Dove D e il quarto di cerchio racchiuso dalla curva Abbiamo due possibilit a primo modo vediamo il quarto di cerchio come dominio normale rispetto a uno degli assi, per esempio D= f(x;y) 2R2 0 x 1;Ii) qual e la probabilit a che il punto si trovi fuori del cerchio di centro (0;0) e raggio 1?X2 y2 dxdy = Z 1 0 •Z 2 1 ‡ x2 y2 dy ‚ dx = = Z 1 0 • x2y 1 3 y3 ‚2 1 dx = Z 1 0 µ x2 7 3 ¶ dx = • 1 3 x3 7 3 x ‚ 0 = 8 3 c) Consideriamo l'integrale Z › xydxdy, dove › = n (x;y) 2 R2 0 < x < 1;
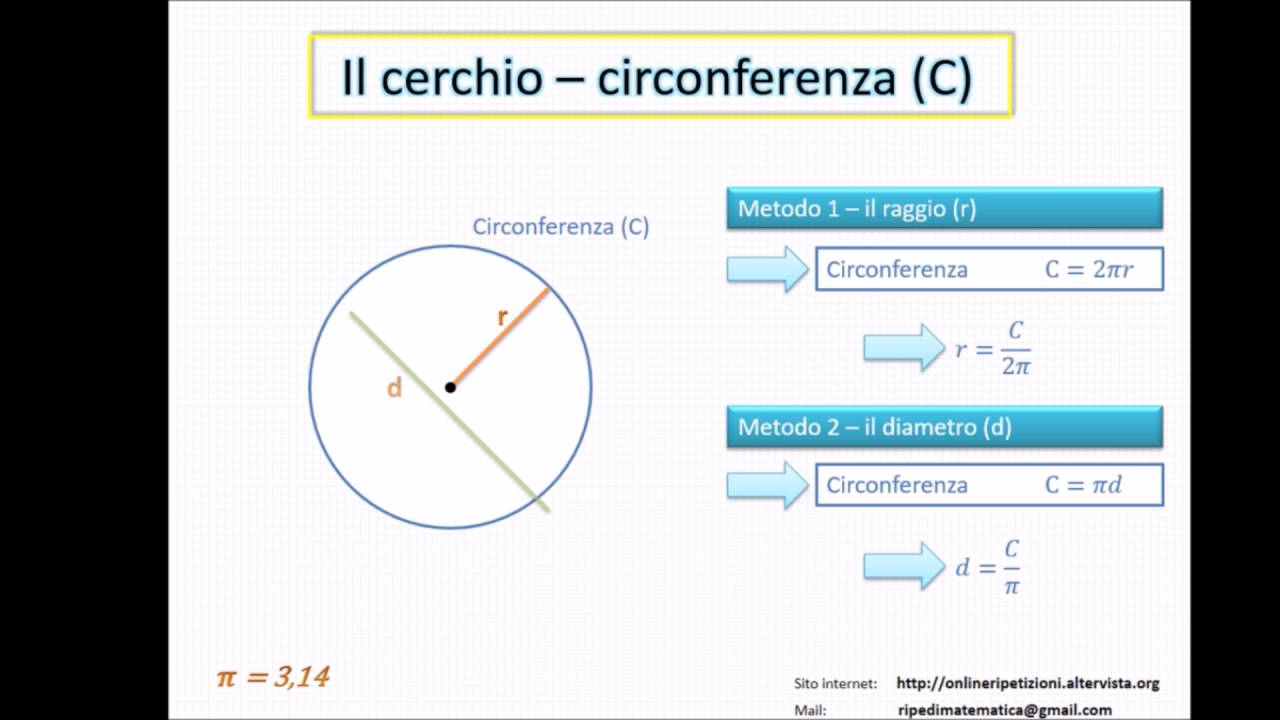
Cerchio Formule Area E Circonferenza Youtube
Formula cerchio x^2+y^2
Formula cerchio x^2+y^2-$$ (x3)^2(y2)^23=0 $$ e una retta $$ 2x5y6=0 $$ Devo capire se la retta è secante, tangente o esterna Per prima cosa, trasformo l'equazione della circonferenza nella forma canonica (x 2 y 2)axbxc $$ (x3)^2(y2)^23=0 $$ $$ (x^26x9)(y^24y4)3=0 $$ $$ (x^2y^2)6x4y10=0 $$0 y p 1 x2g da cui ZZ D 12xy (x2 y2 1)2 dxdy= Z 1 0 dx Zp 1 x2 0 12xy




Come Trovare L Equazione Della Circonferenza Redooc
X2 y2 1 @ @y 3x x2 y2 1 dxdy= ZZ D 12xy (x2 y2 1)2 dxdy; C'e' una formula per trovare il centro del cerchio osculatore a una curva senza dover necessariamente risolvere il sistema?X2 < y < p x o x y02 0 02 04 06 08 1 12 14 0 02 04
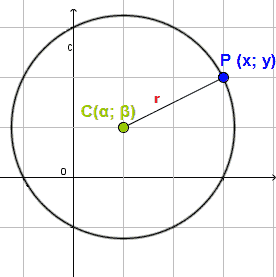
Usare le formule di centro e raggio;I coe cienti di x2 e y2 sono uguali Non e presente il termine misto xy Ci chiediamo ora se un'equazione del tipo x2 y2 axbyc= 0 rappresenta sempre una circonferenza A tale scopo, cerchiamo, se possibile di riscriverla nella forma (1) (x )2 (y )2 = r2 Uguagliando = a 2;L'equazione della nostra circonferenza è x 2 y 2 ax by c = 0 Formule cerchio e circonferenza 1) Per tre punti non allineati passa una ed una sola circonferenza 2) Qualunque corda che non passa per il centro è minore del diametro
corrisponde uno e un solo punto P' e viceversa, e tutti i punti di sono punti uniti, vengono cioè mandati in se stessi dalla trasformazione La trasformazione inversa dell'inversione rispetto al cerchio è l'inversione stessa;Questo formulario è interamente dedicato a circonferenza e cerchio Partendo dalla definizione, elencheremo nel dettaglio tutte le formule del cerchio, comprese le formule inverse, tra cui in particolare quella per calcolare l'area del cerchio e il perimetro, ossia la cosiddetta formula della circonferenza Successivamente analizzeremo tutte le proprietà di cerchio e circonferenza, leE (x2y2)=2 Sia Z = p X2 Y 2 la distanza del punto scelto dall'origine i) Trovare la legge di Z;



Dimostrazione Della Formula Dell Area Di Un Cerchio Attraverso Il Metodo Di Esaustione Algorithms And Math



File Mohr Circle Plane Stress Angle Svg Wikimedia Commons
X 2 y 2 c = 0 x 2 y 2 = r 2 Queste formule possono essere utili nel risolvere alcuni esercizi Ad esempio, quando si possono applicare le formule incomplete non c'è bisogno di trovare tre parametri (a, b, c) per scrivere l'equazione della circonferenza, ma ne sono sufficienti due o addirittura uno soltanto EsempioNella lezione precedente abbiamo visto come possiamo scrivere l'equazione della circonferenza quando conosciamo le coordinate del centro e il raggio In questa lezione, invece, vedremo come, DATA una CIRCONFERENZA, possiamo TROVARE le coordinate del CENTRO e il RAGGIO L'equazione della nostra circonferenza è x 2 y 2 ax by c = 0 x 2 y 2 ax by c = 0 2)Il coefficiente di x 2 è uguale al coefficiente di y 2 e può ridursi uguale all'unità, dividendo l'equazione per tale coefficiente supposto diverso da zero Se i coefficienti di x 2 ed y 2 sono uguali all'unità, l'equazione della circonferenza si dice normale 3)L'equazione manca del termine rettangolare in xy



Equazione Della Circonferenza




A Generalized Power Law Detection Algorithm For Humpback Whale Vocalizations The Journal Of The Acoustical Society Of America Vol 131 No 4
Log ax " 3 x " log ax " 3 x " 3 = ax 1 1 log aa()bc$ =log logbc a, (,bc) log c log log c, b aa= b a (,bc) log aabbn =n$ log , (,bn dR) log log log b b a a c = c ab2 ,,c 0 ac!!11, a21 011a 1 aatz22 tz aatz21 tz y x at az Oz = x 2 t y x at az z = x ( 1 1 t a21 011a 1 log aabc11log bclog aabc12log1)Trovare il centro ed il raggio del cerchio di equazione x2 y2 4x 8y 5 = 0 Tale equazione rappresenta effettivamente la circonferenza, perchè è di secondo grado in x ed y, ha i coefficienti di x2 e y2 uguali fra loro e manca del termine xy2 `e l'arco di circonferenza di equazione x2 y2 = 1 situato nel primo quadrante, si calcoli il lavoro di ~F lungo γ percorsa in verso antiorario Si utilizzi il risultato ottenuto per calcolare l'area della regione C delimitata da γ 8 Utilizzando il teorema di Green, calcolare l'area della regione T ⊂ R2 delimitata dal sostegno




Issuu To Pdf Download Tool




Geometria Piana Formule Del Cerchio
Dalle formule di riduzione otteniamo ZZ 2 x x2 y2 dxdy= Z 1 0 Z x2 1 2 x x x2 y2 dy dx Calcoliamo l'integrale interno con la sostituzione t= y=x, y= xt, dy= xdt, Z x2 1 2 x2 x x 2 y dy= Z x 1 2 x 1 1 t2 dt= arctanx arctan x 2 Dunque ZZ x x 2 y dxdy= Z 1 0 arctanxdx Z 1 0 arctan x 2 dx Una primitiva di arcotangente si troav= ax 2 1 y O x R;Disegniamo un cerchio di raggio 1 Rappresenta il luogo dei punti che hanno la stessa distanza dall'origine, in formule (x,y)x2 y2 = 1 ( x, y) x 2 y 2 = 1 Consideriamo adesso una retta parallela all'asse y e passante per l'asse x, cioè tutti i punti (x,y)x= 1 ( x, y) x = 1 Vogliamo individuare la posizione di un punto P che si trova



Circle Circle Intersection Points Stack Overflow



Equazione Della Circonferenza
Esercizio 2b4 Sia Y una va con legge esponenziale di parametro X;Ove X e una va con legge Gamma di parametri e Qual e la legge di Y?Vorrei usare questa formula d = sqrt ( (circle_x x)^2 (circle_y y)^2) Quindi, confronta semplicemente il risultato di quella formula, la distanza ( d ), con il radius Se la distanza ( d) è inferiore o uguale al raggio ( r ), il punto si trova all'interno del cerchio (sul bordo del cerchio




Geometria Analitica Imathematica




Come Si Calcola La Circonferenza
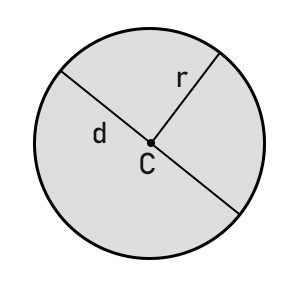
x^2 y^2 ax by c = 0 Se il centro della circonferenza è l'origine (0,0), l'equazione diventa x^2 y^2 = r^2 La circonferenza con centro nell'origine e raggio unitario è chiamata circonferenza goniometrica L'equazione di un cerchio invece è data da x^2 y^2 _ r^2 Circonferenza nel piano complessoL'intersezione fra un angolo al centro, cioè un angolo avente come vertice il centro del cerchio, ed il cerchio stesso (visivamente, uno "spicchio" di cerchio) si chiama settore circolare Se l'angolo al centro è retto, il settore circolare che individua si chiama quadrante;R2 = a2 4 b2 4 c Poich e il raggio e un numero




Felge Schlauchlos Sip Fur Vespa 50 125 Pv Et3 Pk




Circonferenza Come Luogo Geometrico Esercizi Docsity
Sostituendo nella generica circonferenza ho x2 y2 4x c=0 Mettendo a sistema la circonferenza e la retta tangente x2 y2 4x c=0 2 x2 4 c = 0 ⇒ y = x2 y = x2 ⇒ per la condizione di tangenza ∆ = 0 ⇒ 8 (4c) = 0 ⇒ c = 4 e quindi x2 y2 4x Œ 4 =0Per estensione si definisce raggio di un cerchio o di una sfera anche la lunghezza di un tale segmento Il raggio misura la metà del diametro Più generalmente — in geometria , ingegneria , teoria dei grafi , e in molti altri settori — il raggio di qualcosa (per esempio di un cilindro, di un grafo , o di un componente meccanico) è laX^2y^2=3^2 La somma del quadrato dei cateti è il quadrato dell'ipotenusa (x,y) sono le coordinate dei punti che soddisfano l'equazione sull'asse cartesiano Inchioda uno spago di lunghezza 3 all'origine Tienilo dall'altra parte Alle dita avrai il




Area E Perimetro Del Cerchio Formule Ed Esercizi Geometria Imparare Facile



Java Cannot Make A Static Reference To Non Static Field Stack Overflow
Cerchio nel piano cartesiano Per descrivere un cerchio nel piano cartesiano è sufficiente conoscere l'equazione della circonferenza che lo delimita se, ad esempio, avessimo una circonferenza data dall'equazione per individuare tutti e soli i punti interni alla circonferenza ci basterà scrivere la disequazioneFormula per il cerchio x2 y2 = r2 Formula per la linea di tangenza che passa attraverso il punto A (x', y') y – y' = m (x – x') * m rappresenta la pendenza della linea di tangenza Con questo programma, la pendenza m e l'intercetta b (= y' – mx') sono ottenute per linee tracciate dal punto A (x', y') e sono tangenti ad un cerchio conParabola L'equazione più semplice per una parabola , y = X 2 {\ displaystyle y = x ^ {2} \,} può essere (banalmente) parametrizzato utilizzando un parametro libero t e l'impostazione X = t , y = t 2 f o r ∞ < t < ∞ {\ Displaystyle x = t, y = t ^ {2} \ quad \ mathrm {per} \ infty



Perimetro Cerchio Formule E Calcolo Con Il Metodo Semplificato




Formule Geometria Analitica Del Piano Cerchio E Circonferenza Note Le Coordinate Del Centro E Di Un Punto Sulla Circonferenza
2) 12 x 2 y 2 4x 2y 0, r x 2y 5 0 tangente ( 1;Algebra Tracciare x^2y^2=9 x2 y2 = 9 x 2 y 2 = 9 Questa è la formula di un cerchio Usare questa formula per determinare il centro e il raggio del cerchio (x−h)2 (y−k)2 = r2 ( x h) 2 ( y k) 2 = r 2 Confrontare i valori in questo cerchio con quelli nella forma standard La variabile r r rappresenta il raggio del cerchio, h hCiò significa che, componendo un'inversione con se stessa, otteniamo l'identità



L Equazione Del Cerchio Mathcracker Com
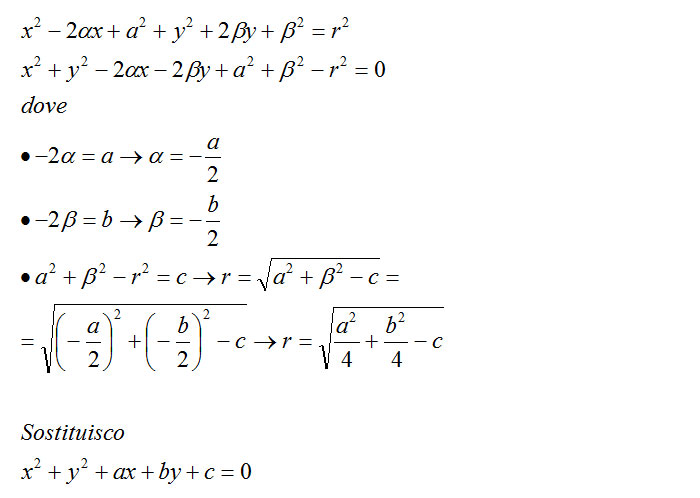



Equazione Della Circonferenza Formula Ed Esercizi Svolti
La precedente formula si dimostra con la costruzione del cerchio osculatore La generica circonferenza di centro $C(C_x,C_y)$ e raggio $r$ ha equazione $(xC_x)^2è uguale a uno Questa parametrizzazione dà lo stesso valore per la curvatura, poiché equivale alla divisione per r 3 sia al numeratore che al denominatore nella formula precedente Lo stesso cerchio può essere definito anche dall'equazione implicita F ( x , y ) = 0 con F ( x , y ) = x 2 y 2 r 2 Quindi, la formula per la curvatura inE il cerchio è (Cx x) ^ 2 (Cy y) ^ 2 = R ^ 2 se sostituisci le formule xey della linea nella formula cerchi ottieni un'equazione di secondo ordine di t e le sue soluzioni sono i punti di intersezione (se ce ne sono)



Hal Archives Ouvertes Fr Hal Document




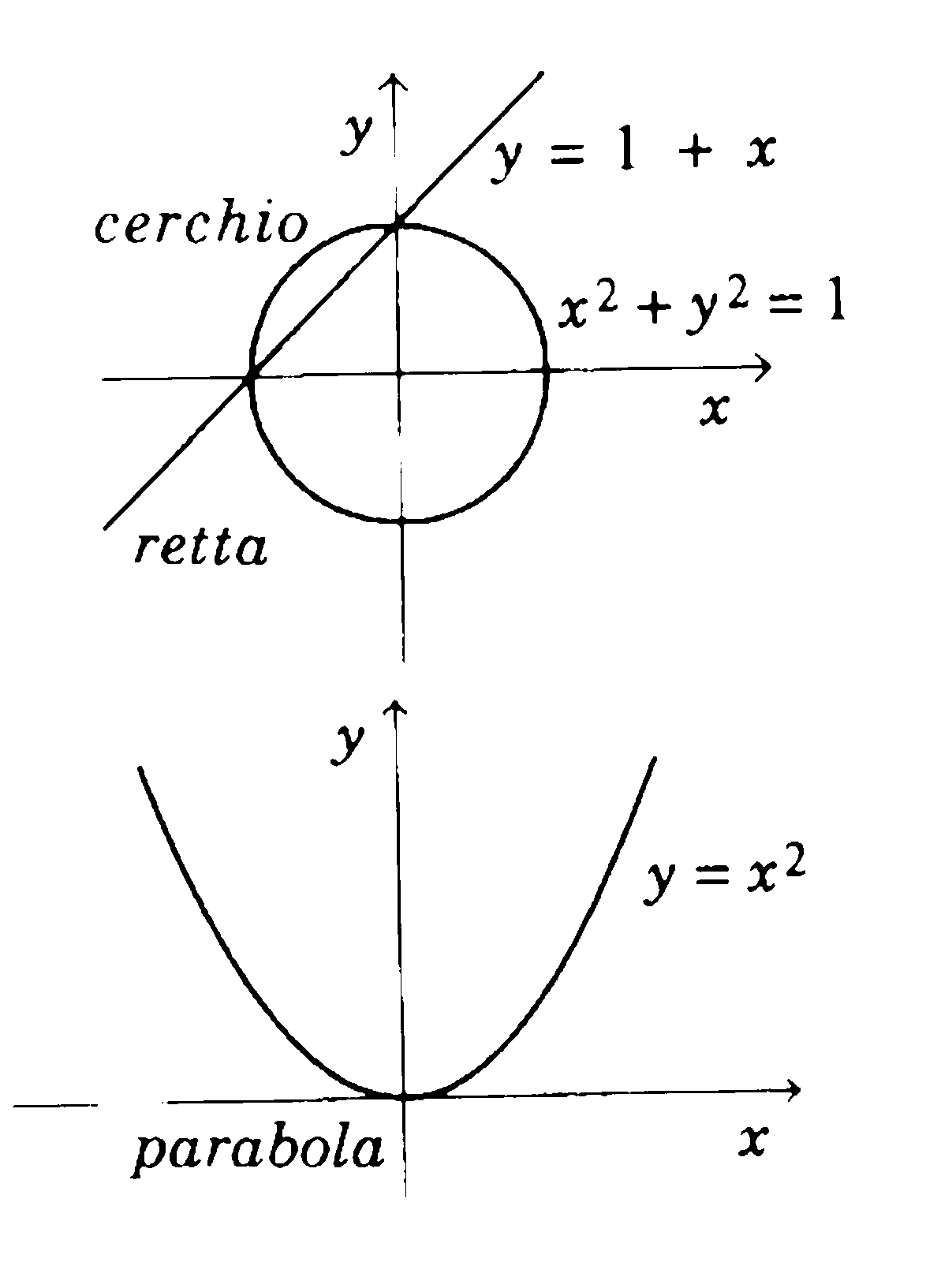
X 2 Y 2 1 E X 2 Y 2 1
#x^2y^2=16# Nota che possiamo riscrivere questa equazione come #(x0)^2(y0)^2 = 4^2# Questo è nella forma standard #(xh)^2(yk)^2 = r^2# di un cerchio con il centro #(h, k) = (0, 0)# e raggio #r = 4# Quindi questo è un cerchio di raggio #4# centrato sull'origine grafico {x ^ 2 y ^ 2 = 16 10, 10, 5, 5}3) 11 10 9Appunto di geometria per le scuole superiori che descrive cos'è la circonferenza, l'equazione della circonferenza e altre regole ed esercizi




Equazione Del Cerchio Studenti It
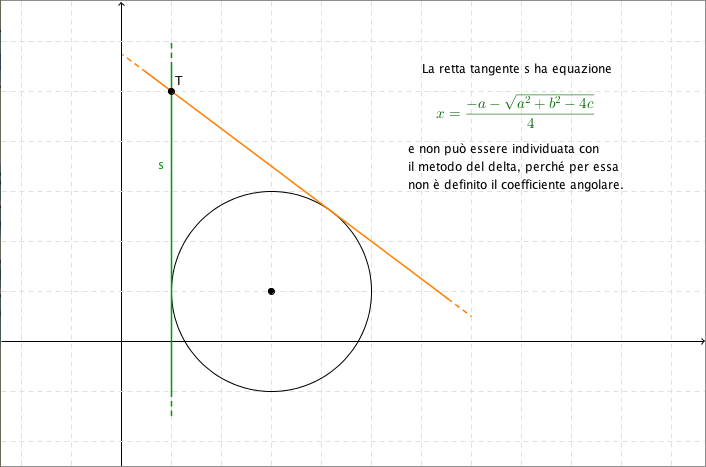



Equazione Della Circonferenza E Formule Del Piano Cartesiano Coniche Weschool
Portare l'equazione canonica nella forma \((xx_c)^2 (yy_c)^2 =r^2 \) tramite il metodo del completamento dei quadrati, e da qui leggere semplicemente centro e raggio come visto sopra;Usando Pitagora finiresti con l'equazione data dove in realtà è il 4 r2 Per ottenere i punti della trama manipolare l'equazione come di seguito Dato x2 y2 = r2 → x2 y2 = 4 Sottrarre x2 da entrambe le parti dando y2 = 4 − x2 Prendi la radice quadrata di entrambi i lati y = √4− x2Se si ha l'equazione della circonferenza e bisogna trovare le coordinate del centro e la misura del raggio, bisogna applicare due formule misura del raggio = √(a^2/4b^2/4c) coordinate del




Proporzionalita Quadratica Inversa Grafico



La Circonferenza Goniometrica
Es data la funzione y = 2x^3 x^2/5 1 prendo un punto, mettiamo P(1,14/5 il raggio di curvatura nel punto indicato è R = (1 y'^2)^(3/2)/ABS(y'') = 809*v809/1450 ora facendo il sistema con la circonferenza genericaDato che il tuo scopo è quello di calcolare la lunghezza della circonferenza di un cerchio, devi risolvere l'equazione data in base alla variabile C Moltiplicando entrambi i membri dell'equazione per 2r otterrai π x 2r = (C / 2r) x 2r, che semplificando è come scrivere 2πr = C Determina l'equazione della circonferenza avente come diametroIntere interni ad una circonferenza di equazione del tipo x 2y = n, centrata nell'origine degli assi, ossia il numero di soluzioni intere delle disequazioni del tipo x 2y n Lo scopo di questo approfondimento è lo studio del numero di soluzioni intere delle disequazioni del tipo x2 y2 n, noto come Il problema del cerchio di Gauss



Circonferenza E Cerchio




Gtsport Livery Search Engine
Questo strumento è in grado di fornire Raggio del cerchio con centro all'origine (0,0) calcolo con le formule associate ad essoX 2 y 2 2x 4y 6 0, r y x 1 0 esterna x 2 y 2 4x 6y 9 0, r y 1 0 tangente ( 2;So, the equation becomes (2) x^2 y^2 A * x B * y C = 0 Although (2) is more compact, (1) is what is more useful for programming, as center points and radius can be obtained directly Equations for drawing a circle Equations (1) or (2) are given in the implicit form That means, those cannot be used for drawing a circle




X 2 Y 2 Formula X 2 Y 2 Z 2 Xy Yz Zx Formula Luar Biasa




A Generalized Power Law Detection Algorithm For Humpback Whale Vocalizations The Journal Of The Acoustical Society Of America Vol 131 No 4
Il questo video si spiega come trovare le coordinate del centro e il raggio di una circonferenza data la sua equazione I metodi illustrati sono due quello classico di applicazione delle formule e quello del completamento dei quadrati Quest'ultM = 03 P Equazione della retta y=03x5 Modifica il valore di m per visualizzare le diverse rette del fascio per il punto P Esistono due rette passanti per P e tangenti alla circonferenza Mettiamo dunque a sistema fascio e circonferenza { x 2 y 2 − 3 y − 4 = 0 y = m ( x − 0) 5 Sostituiamo nell'equazione della circonferenza laRicaviamo quindi le formule di centro e raggio dall'equazione in forma canonica \(x^2y^2axbyc=0\)



2




3 Modi Per Trovare Il Raggio Di Una Sfera Wikihow
`x^2y^22ax2byc=0 , c=a^2b^2r^2` Raggio `r=sqrt(a^2b^2c) , a^2b^2c>0` Condizione di realtà `a^2b^2c>0` L' asse radicale di due circonferenza è la retta che passa per i loro punti di intersezione Date due circonferenze di equazione `x^2y^22ax2byc=0` e `x^2y^22a_1x2b_1yc_1=0`, l'equazione dell'asse radicale èTrovare le Proprietà x^2y^2=25 Questa è la formula di un cerchio Usare questa formula per determinare il centro e il raggio del cerchio Confrontare i valori in questo cerchio con quelli nella forma standard La variabile rappresenta il raggio del cerchio, rappresenta lo spostamento xSe è piatto, è il semicerchio



1
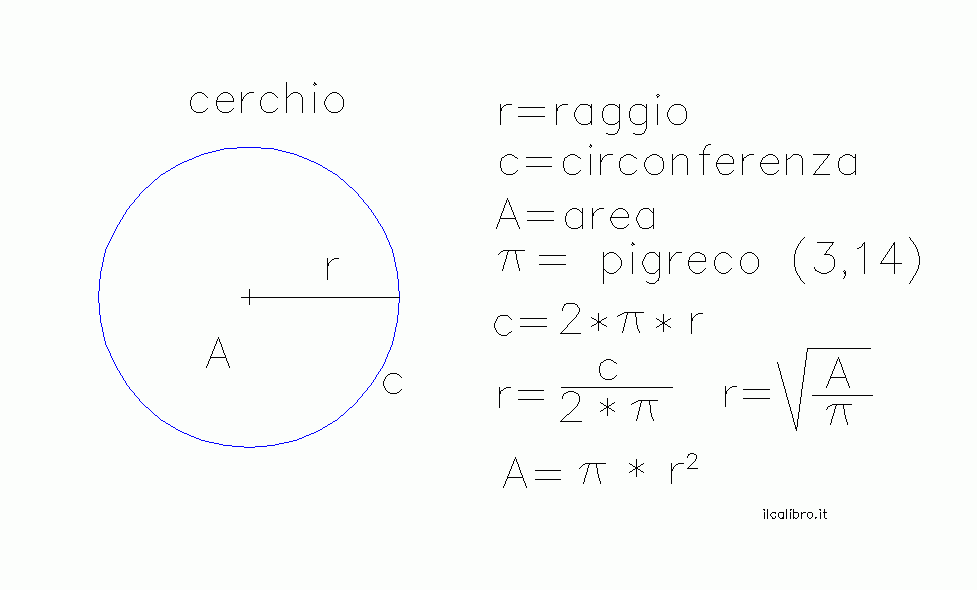



Geometria Piana Formule Del Cerchio
1) x 2 y 2 6x 5 0, r x y 3 0 secante ( 3 2;Imposto sistema equazioniretta e cerchio x^2y^2axbyc=0 y = mxq ( axbyc=0) esepro1 calcolare e disegnare grafico soluzione con geogebra, derive, cabri, excel esepro1geo (nessun calcolo richiesto a utente) esepro1derive (calcoli eseguiti con funzioni di




Gtsport Livery Search Engine




Come Trovare L Equazione Della Circonferenza Redooc



Area Del Settore Circolare




Geometria Analitica 2 I Blog Di Alessio Empoli




Agonism Antagonism And Inverse Agonism Bias At The Ghrelin Receptor Signaling Journal Of Biological Chemistry



Home Aero Polimi It Lastaria Archivio 15 Curve 1 Pdf




Pin Su Matematica



Le Rette Tangenti Condotte Da Un Punto P Ad Una Circonferenza Possono Essere O Due O Una Sola A Seconda Se Il Punto P E Estern



Circonferenza




Cerchio Formule Area E Circonferenza Youtube



Geometria Analitica Su P C




Pin On Matematyka Wzory Etc



1




Area E Perimetro Del Cerchio Formule Ed Esercizi Geometria Imparare Facile
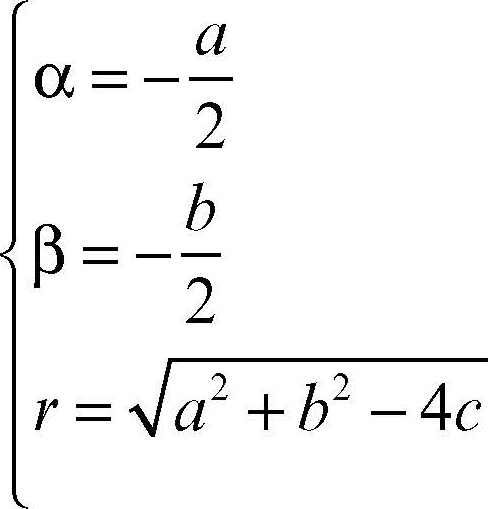



Circonferenza In Enciclopedia Della Matematica



Discovering The Midpoint Formula Geogebra



1




Formule Del Cerchio Scuolissima Com




X 2 Y 2 Formula X 2 Y 2 Z 2 Xy Yz Zx Formula Luar Biasa




Calcolo Di Area E Perimetro



Q Tbn And9gcssdgxfplwf2nwwz5f0tzqny Kihndoweoac3gpvtdo22ss Usqp Cau



2



Calcolo Coordinate Punti Di Contatto Tra Parabola Asse Verticale E Circonferenza




Circonferenza



Un Corso Elementare Di Calcolo Infinitesimale Segue Che Questo E Identico Tranne Che Per La Notazione Con La Formula 2 Dell Art 152 406 Calcolo Infinitesimale Ch X 154 Cerchio Di Oscillazione Un Modo



Oltre Il Compasso




Cerchio Di Apollonio Wikipedia
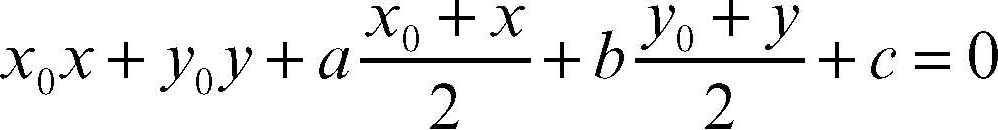



Circonferenza In Enciclopedia Della Matematica




La Superformula Di Johan Gielis



Miky Genny Geometria Circonferenza E Complementi




7 Lunghezza Circonferenza E Area Cerchio



Descrizione Teorica Elementare Della Circonferenza



Cerchio Ed Ellisse



Miky Genny Geometria Circonferenza E Complementi




06 Quadratura Del Cerchio Leggendo Archimede




Circonferenza E Cerchio Tutte Le Formule Redooc



2 Algoritmi In Vb Per La Circonferenza Con Il Centro Su Xc Yc



Le Rette Tangenti Condotte Da Un Punto P Ad Una Circonferenza Possono Essere O Due O Una Sola A Seconda Se Il Punto P E Estern



Honda Xl 125 V Varadero Jc32 Felge Vorne Vorderrad Wheel Rim Cerchio Ebay




Come Calcolare Circonferenza E Area Di Un Cerchio




Lineaeffe 21 En By Oleg Kadnikov Issuu




La Circonferenza
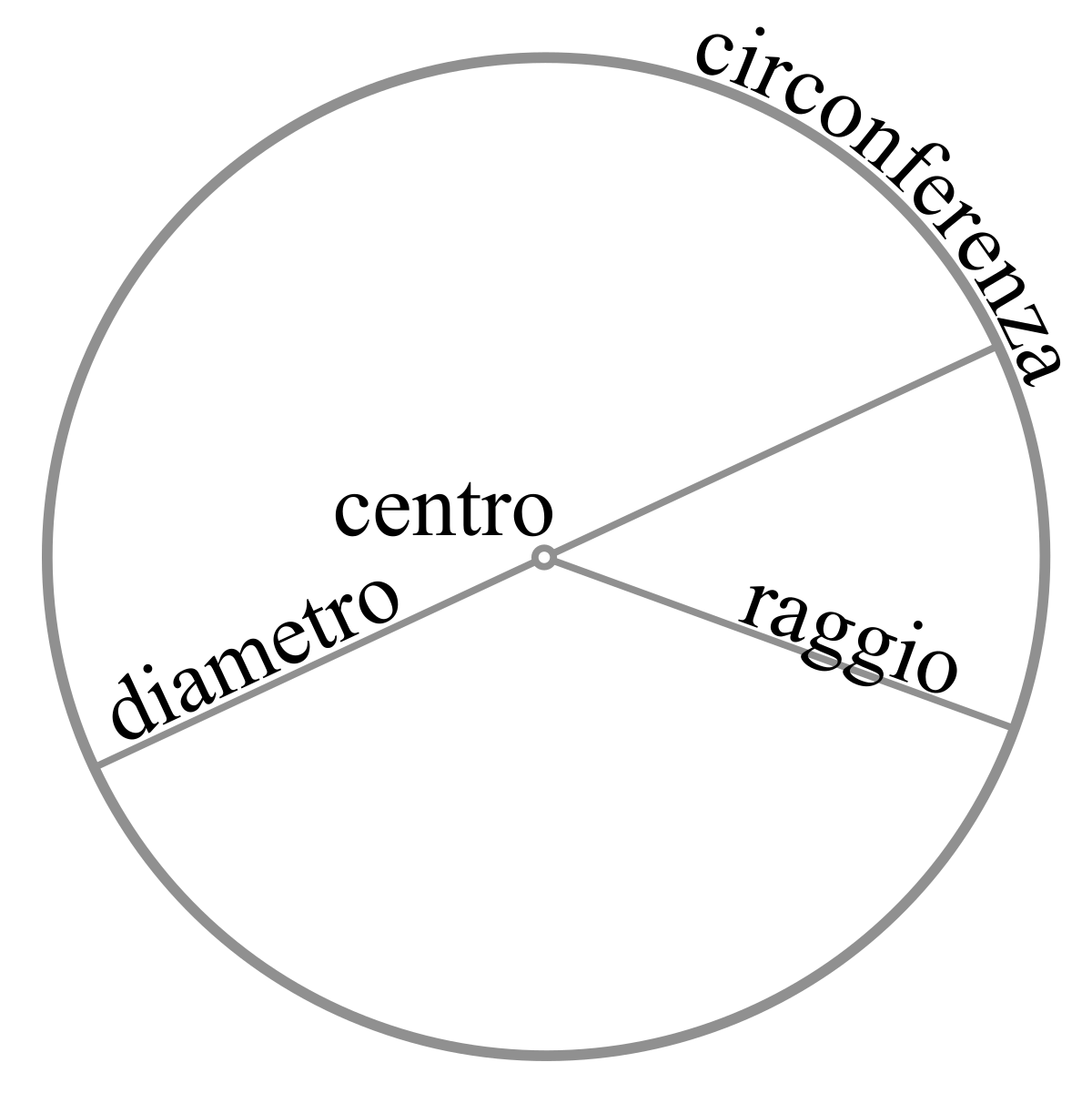



Cerchio Wikipedia
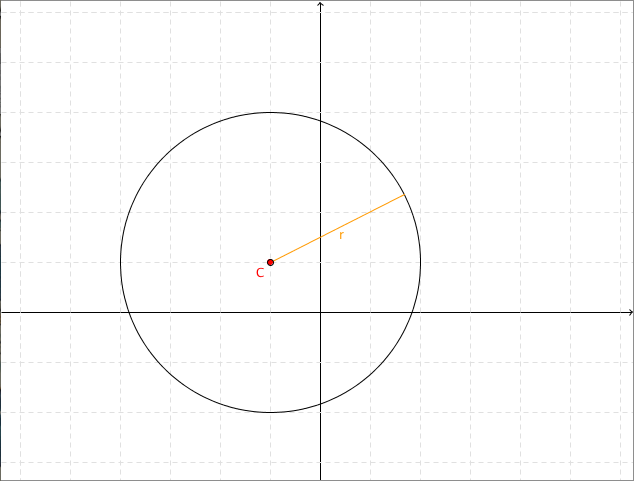



Equazione Della Circonferenza E Formule Del Piano Cartesiano Coniche Weschool



Cerchio Di Superficie Doppia Geogebra




Circonferenza




Come Calcolare Circonferenza E Area Di Un Cerchio




Come Calcolare La Distanza 8 Passaggi Con Immagini




Equazione Della Circonferenza




Come Calcolare L Area Del Cerchio Youtube




Michelin 3 50 10 59j Tl Tt S Rf Motorradreifen Amazon De Auto Motorrad




3 Ways To Calculate The Diameter Of A Circle Wikihow
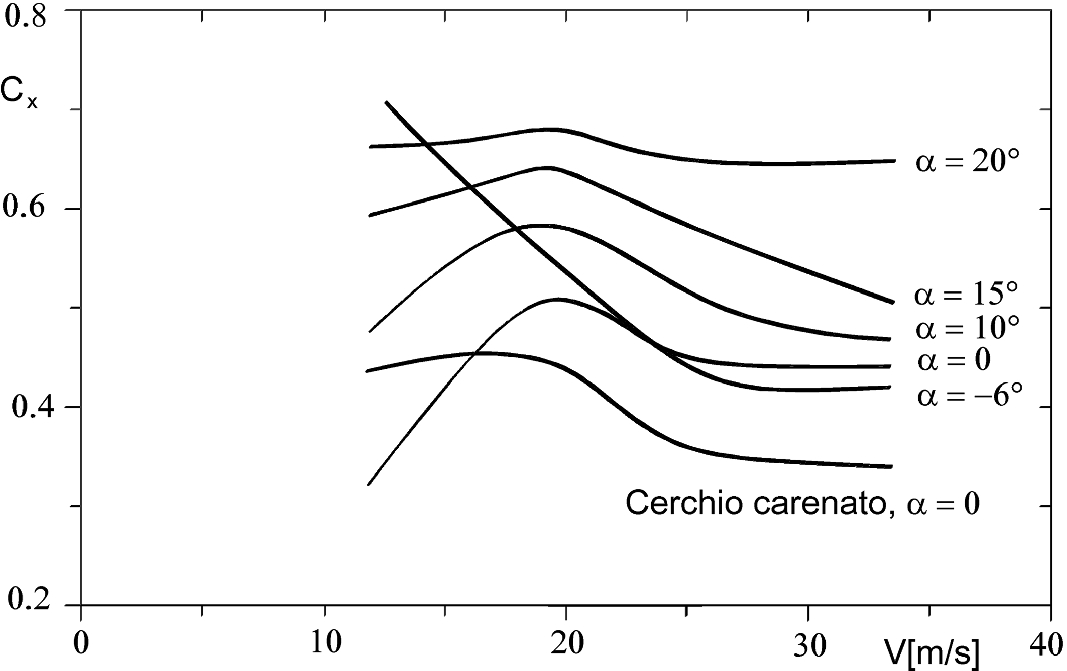



An Overview On Motor Vehicle Aerodynamics Springerlink



La Bella Geometria Classe Terza Circonferenza E Cerchio




Equazione Della Circonferenza Per Superiori Redooc



Miky Genny Geometria Circonferenza E Complementi




Pdf Birth Growth And Computation Of Pi To Ten Trillion Digits



Equazioni Della Tangente Condotta Da Un Punto Sulla Circonferenza



Formule Del Cerchio Area Settore Circolare Diametro Raggio Corda Weschool



La Circonferenza Come Calcolare Il Raggio E Le Coordinate Del Centro Mediante Equazioni E Formule Weschool



Problema Con Ellisse E Iperbole 1 Svolgomath It




Come Calcolare Circonferenza E Area Di Un Cerchio



Elearning Uniroma1 It Mod Resource View Php Id




Matematicamente It Esercizio Con Una Superficie Che Dovrebbe Essere Regolare Leggi Argomento




Geometria Analitica 2 I Blog Di Alessio Empoli




Circonferenza Per Due Punti Con Centro Su Una Retta



Hal Archives Ouvertes Fr Hal Document



Miky Genny Geometria Circonferenza E Complementi



Www Bast De Druid En Deliverales List Downloads Deliverable 1 1 2 B Pdf Blob Publicationfile V 1




Cerchio Wikipedia




Pdf Matematica E Applicazioni



Is Cetirizine A Sulfa Drug Order Generic Online Without


