
基本の作図 5ステップでわかる 平行移動の書き方 Qikeru 学びを楽しくわかりやすく
グラフの平行移動の証明と例 高校数学の美しい物語 このサイトでは、像の変換(x,y)→(X,Y)を利用して証明しています。もしあなたが理系であれば、これは必ず習得してください。もし数学はそこまで重要な科目でなければ、次のカンタンなことを考えればいいです。例えばxがx軸の右側へ3Q q 平行移動するとき、式は以下のように表すことができる。 y = ( x − p) 2 q y= (xp)^2q y = (x−p)2 q y = ( x − 2) 2 5 y= (x2)^25 y = (x−2)2 5 の 5 5 5 を左辺に移項すると、このような式になります。 y − 5 = ( x − 2) 2 y5= (x2)^2 y−5 =(x−2)2
数学 平行 移動
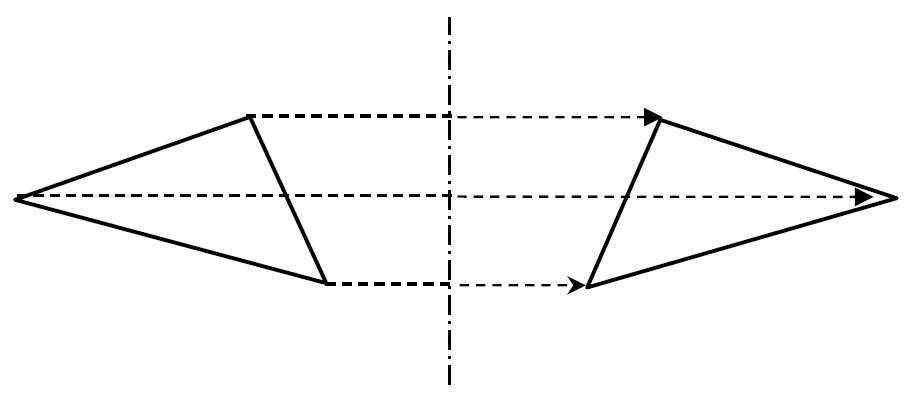
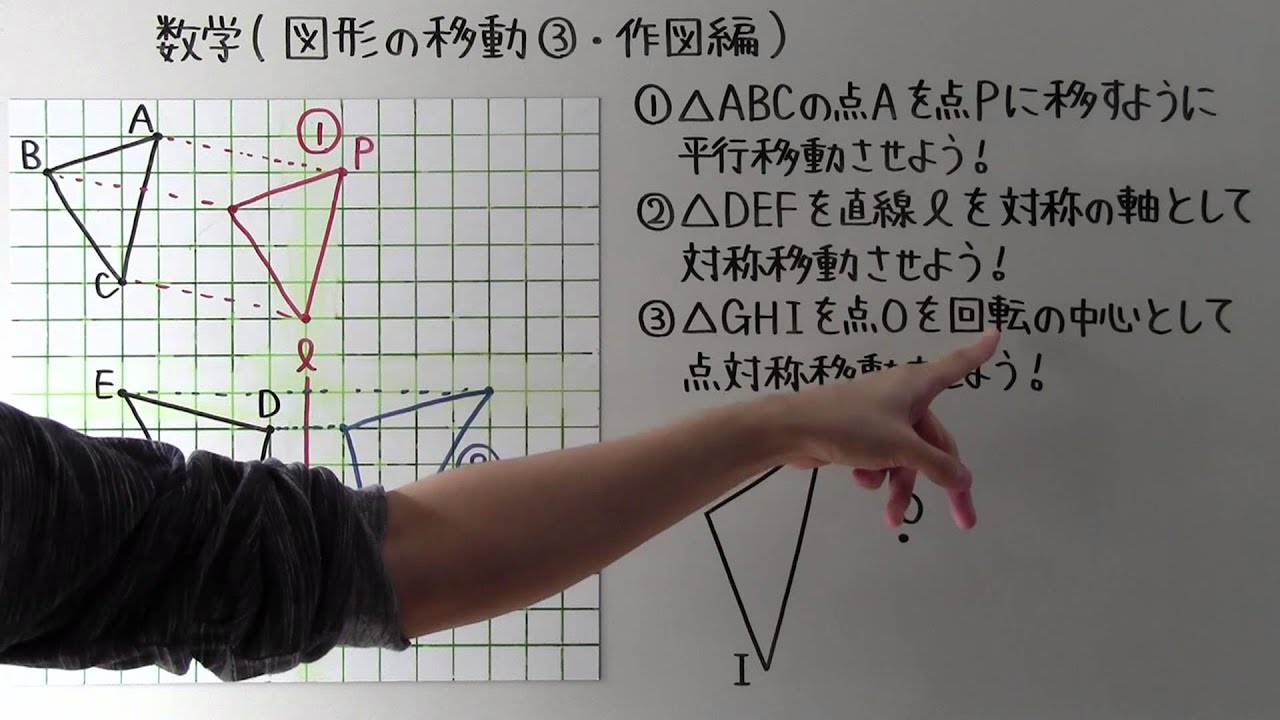
数学 平行 移動-中学校1年生の数学では「図形の移動」について習います。 図形の移動は主に「平行移動」「回転移動」「対称移動」の3種類がありますが、 今回は回転移動について見ていきましょう。 回転移動とはどういったもので、回転移動した図形にはどういった性質があるのか、また図形の回転移動はTranslation 日常では「翻訳」としか訳すことがない translation ですが,数学では「平行移動」という意味があり,移動のさせ方はベクトルで表します.日本の教科書でよく使われる「x軸方向に p ,y軸方向に q 平行移動したもの」という言い方は,a translation of

数学ia 放物線の平行移動 大学入試数学の考え方と解法
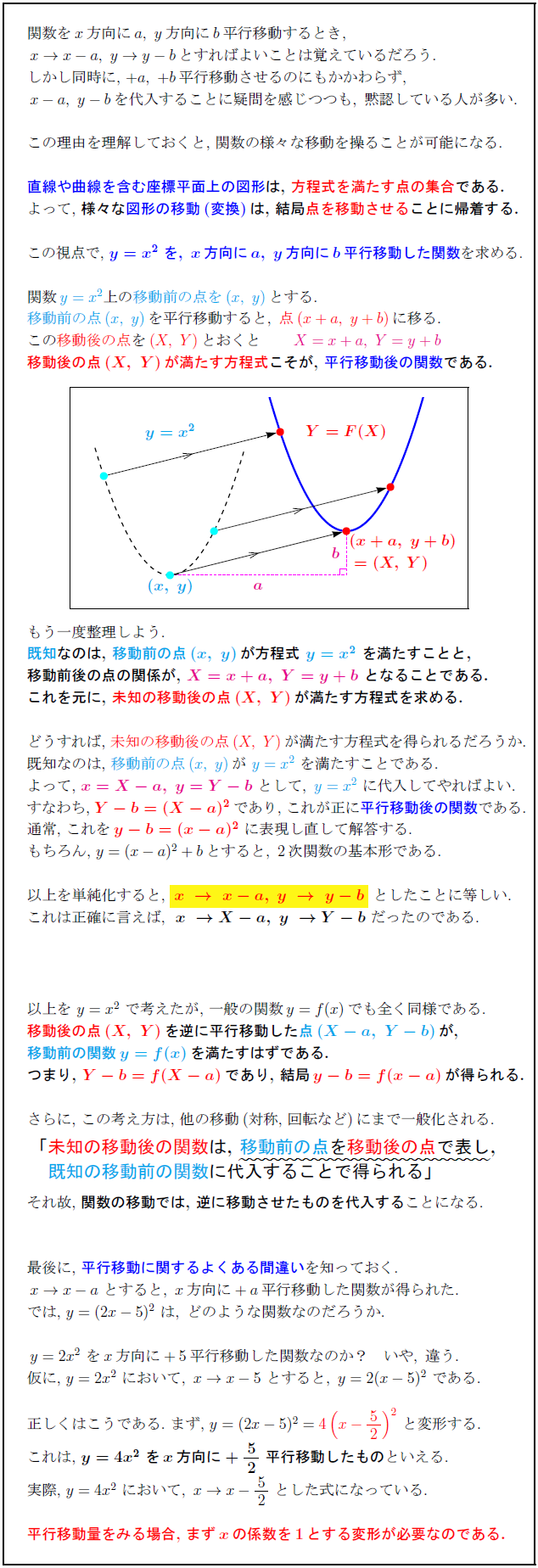
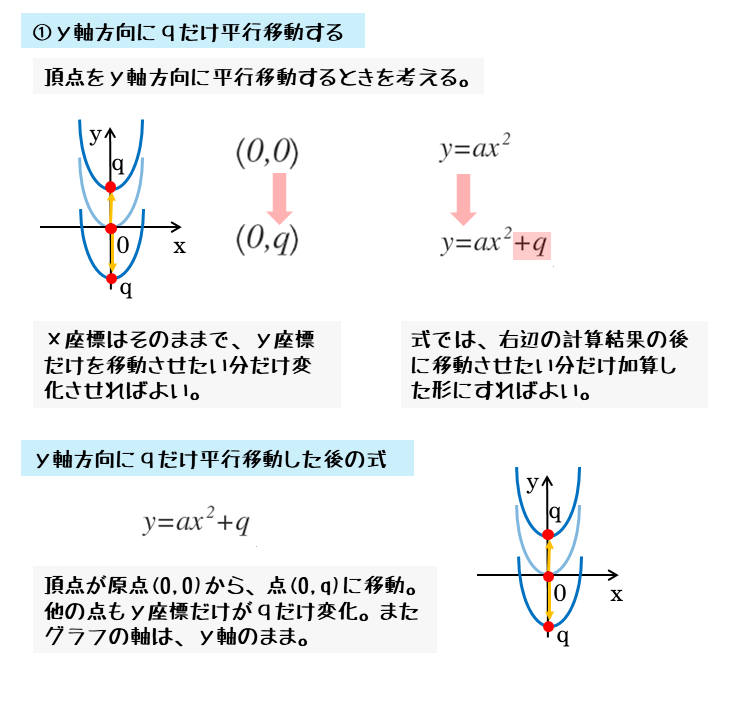
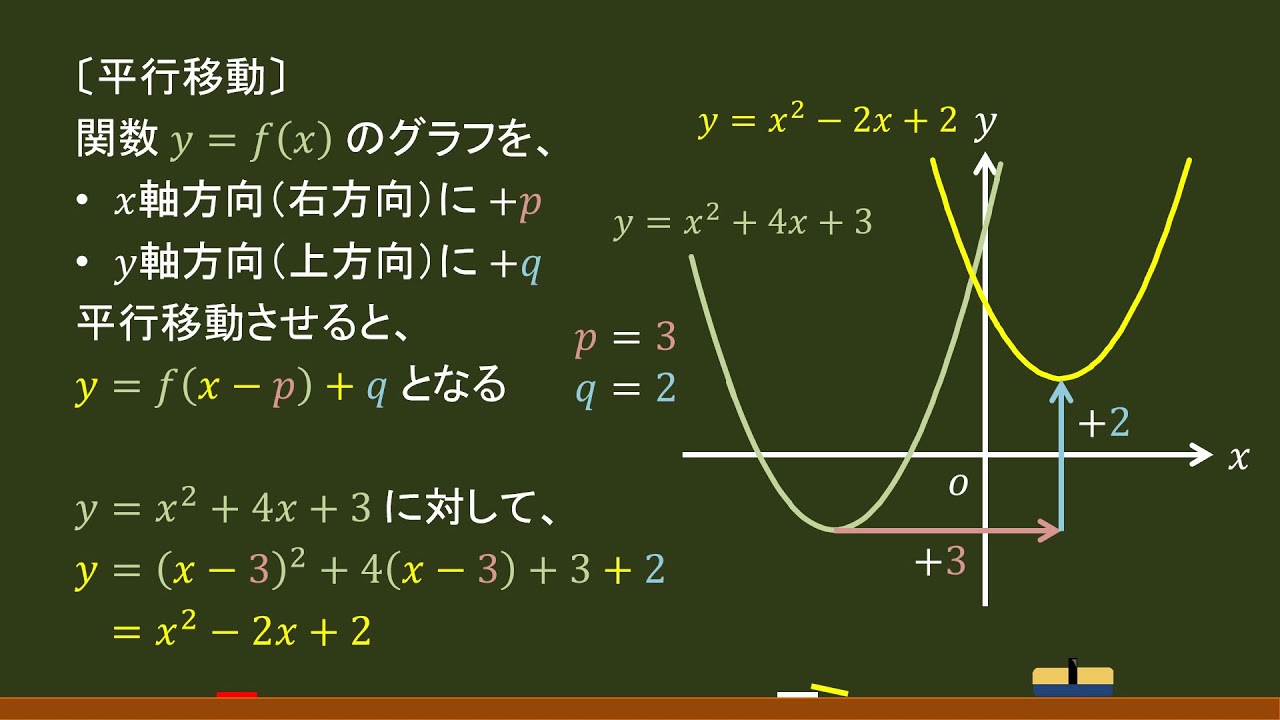
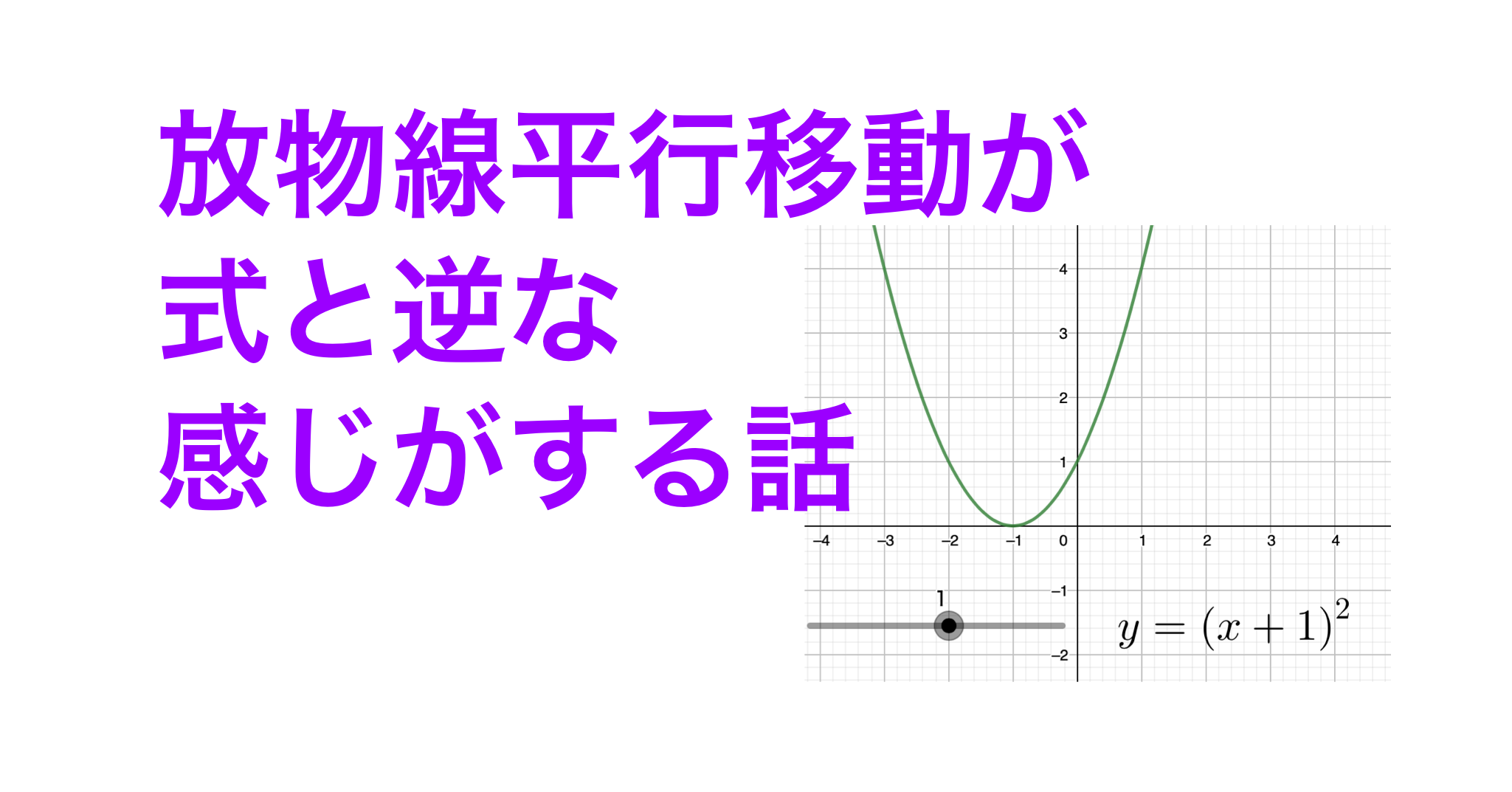
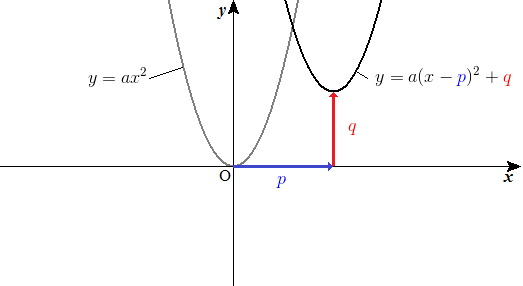
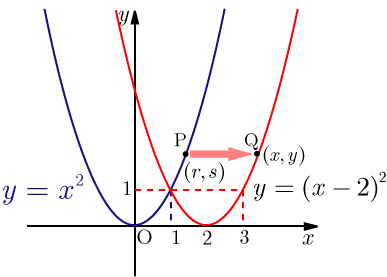
平行移動の公式 \(y=ax^2\)のグラフを,\(x\)軸方向に\(p\),\(y\)軸方向に\(q\)だけ平行移動した放物線は\y=a(xp)^2q\である. カテゴリー 数学Ⅰ タグ 高校数学、数学Ⅰ、平行移動 の公式、高校生、塾、気仙沼、個別指導 投稿ナビゲーション 前の投稿 前 使おう,位置ベクトル 次の投稿平行移動の考え方1 平行移動の考え方2 平行移動の考え方3 x軸方向にp、y軸方向にq移動 は、 x⇒x-p、y⇒y-q に置きかえる (例) y=x 2 をx軸方向にp、y軸方向にq移動したグラフ ↓ y -q =(x -p ) 2 ⇔y=(x-p) 2 +q数学科学習指導案 学 級:1年2組 4平行移動の意味を理解し、操作 平行移動、回転移動、対称移動に関心を持ち、ある図 などを通して基本的な性質を見 形を移動させた図をかこうとしている。 いだす。 〔観察・ノート〕 平行移動、回転移動、対称移動の意味とそれらの基本 5
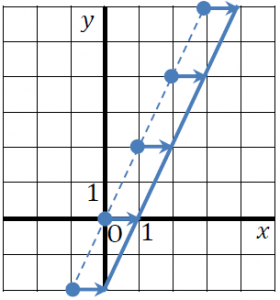
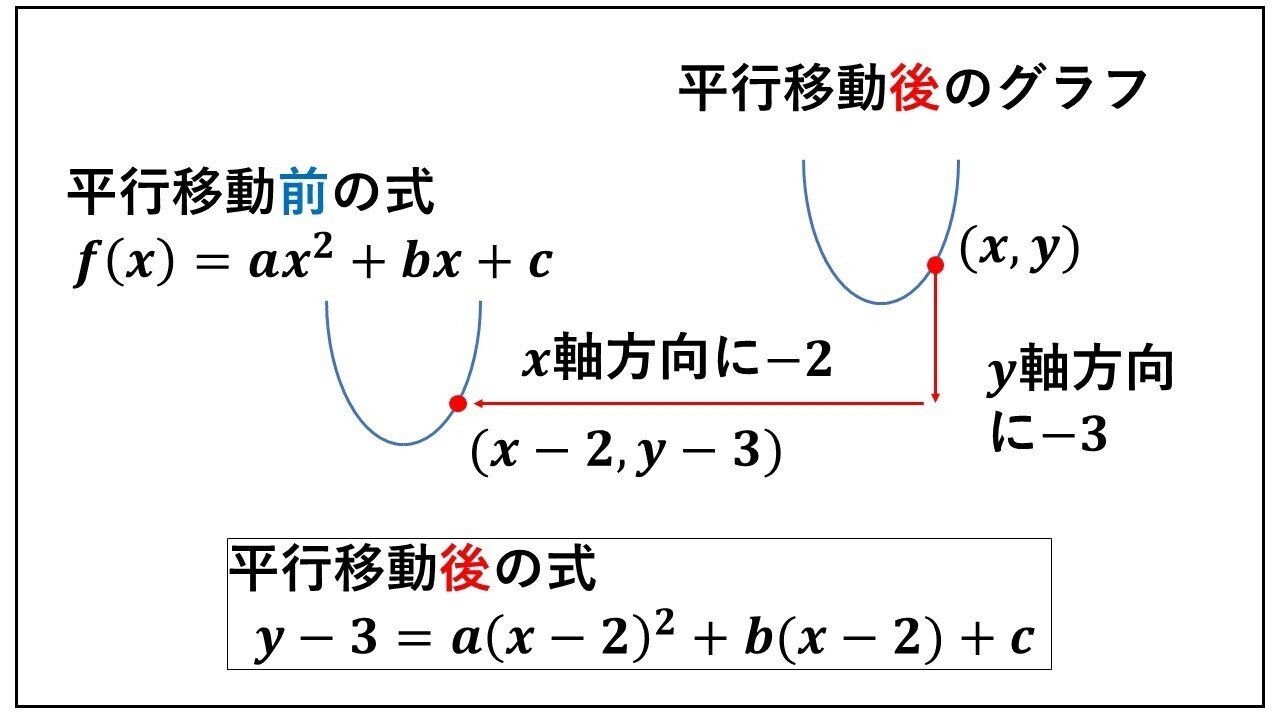
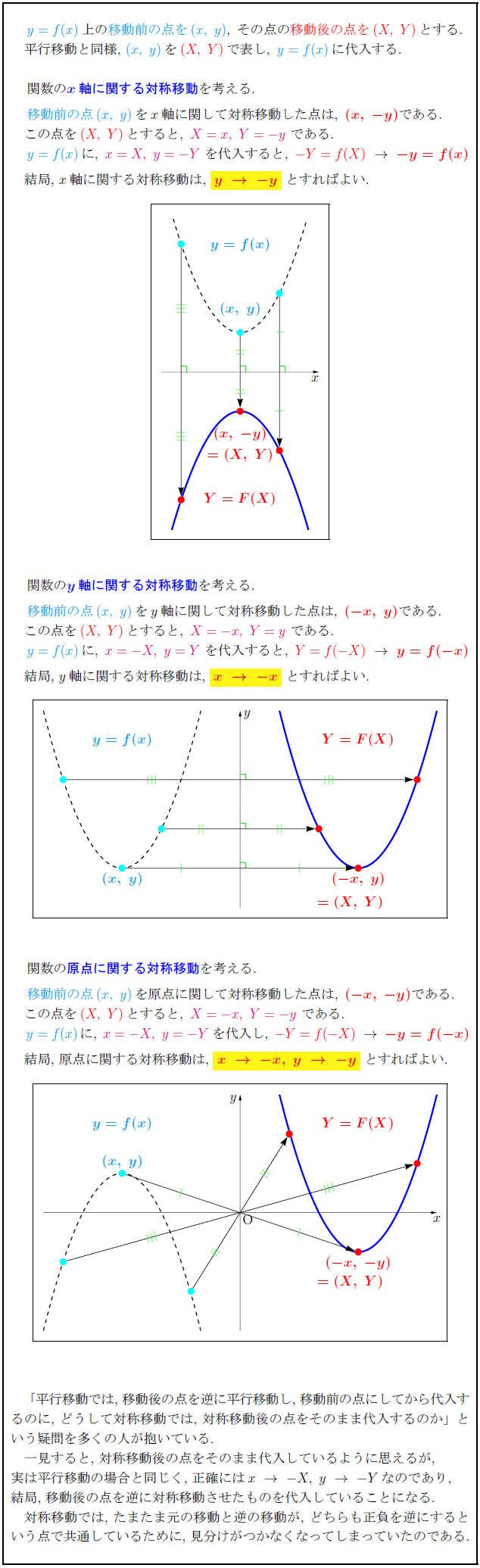
グラフの平行移動とは、 グラフ上のある図形または関数を、形を変えず、一定方向に一定の距離だけ移動させること をいいます。 一般的に、グラフを平行移動させるときには、 \(x\) 軸方向と \(y\) 軸方向にそれぞれ どれだけ移動したかを明記 します。数学Ⅰ 質問(無料公開版 (過去受付分)) 質問数学(2次関数):平行移動で符号が逆? になることについて 〔質問〕 y=x 2 +3x-3 を x軸方向に-3、y軸方向に2だけ移動させた放物線は、なぜ y+2=-2 (x-3) 2 +5 (x-3)+4 ではなく、y-2=-2 (x+3) 2平行移動の構造を見つけたらこの公式を思い出しましょう。 一次関数の平行移動 傾きが p p p で (a, b) (a,b) (a, b) を通る直線の方程式は(原点を通る傾き p p p の直線を平行移動させたものなので), y − b = p (x − a) yb=p(xa) y − b = p (x − a) となります。 二次関数の平行移動
数学 平行 移動のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  | |
 |  |  |
「数学 平行 移動」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「数学 平行 移動」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「数学 平行 移動」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「数学 平行 移動」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  | |
「数学 平行 移動」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「数学 平行 移動」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「数学 平行 移動」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 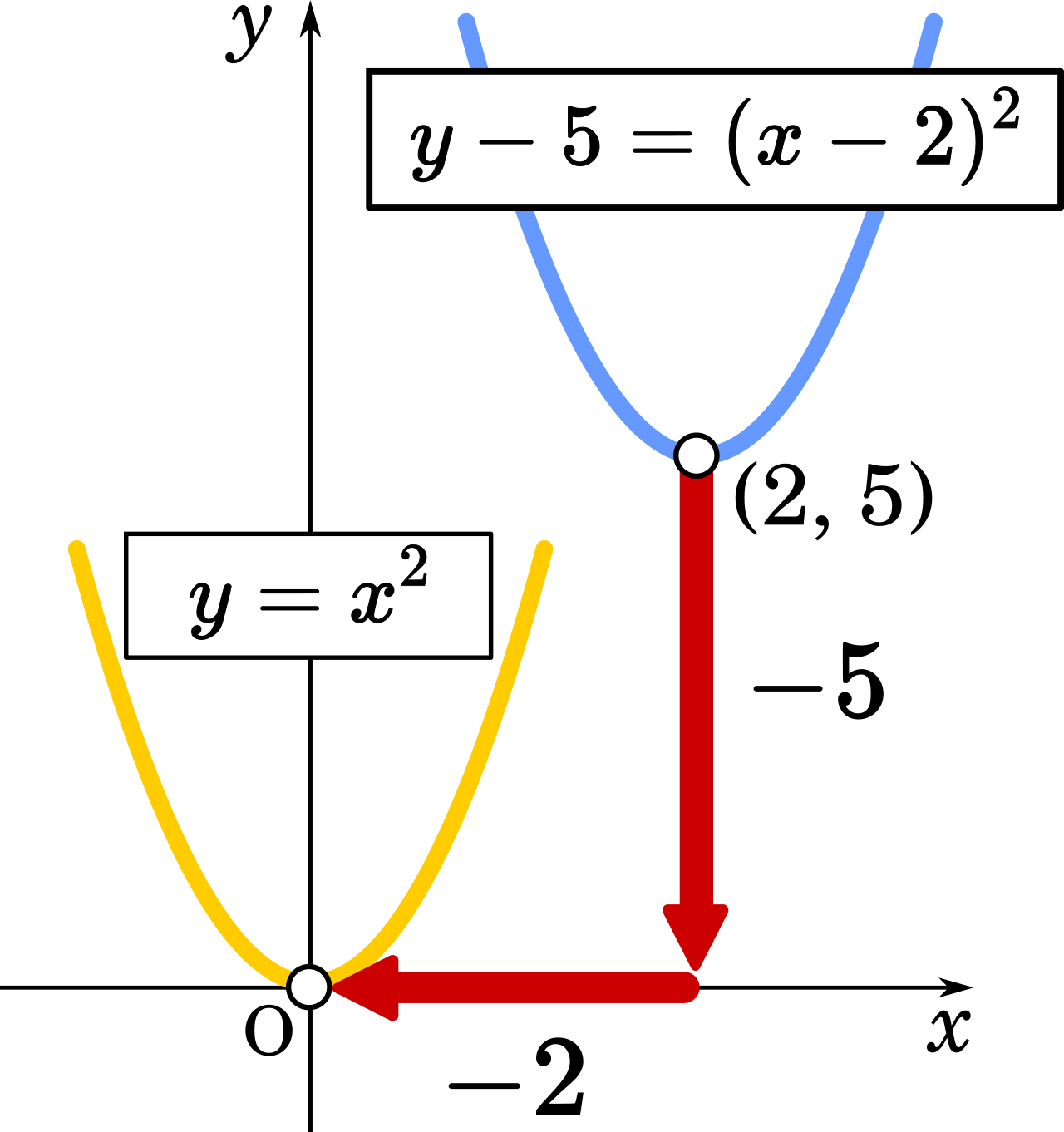 | |
 |  | |
 |  |  |
「数学 平行 移動」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「数学 平行 移動」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「数学 平行 移動」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「数学 平行 移動」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |
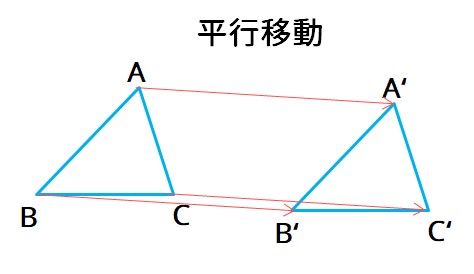
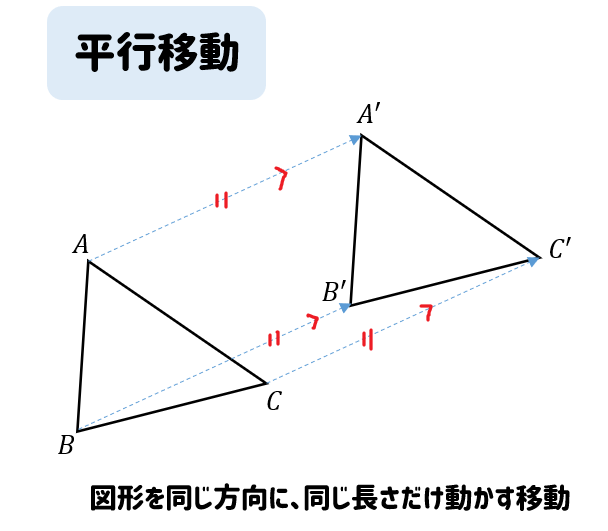
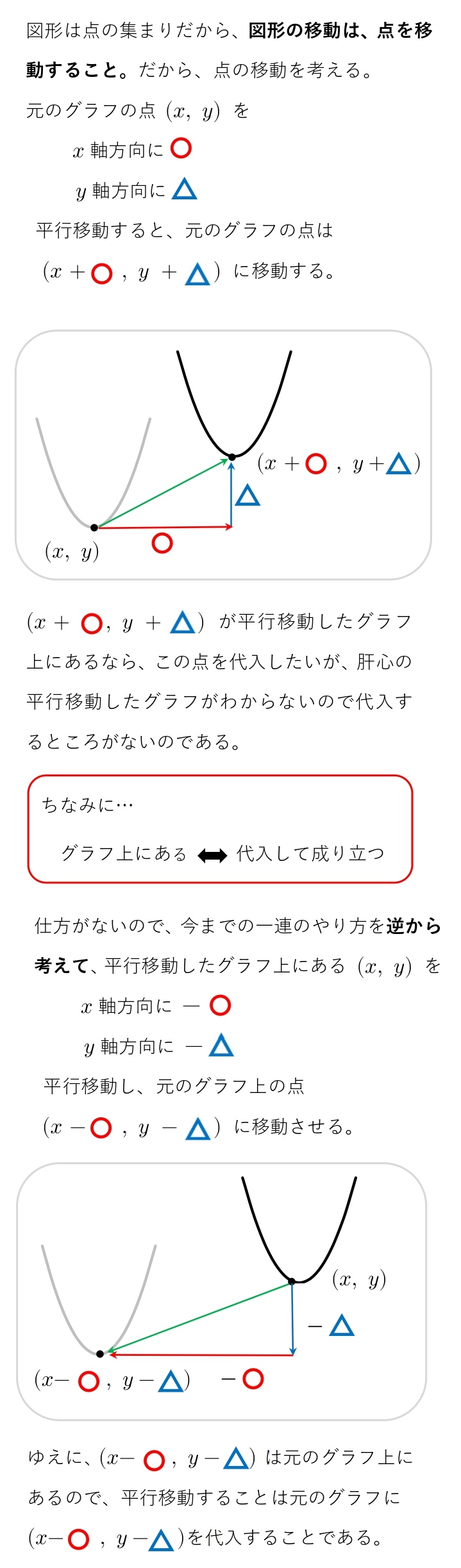
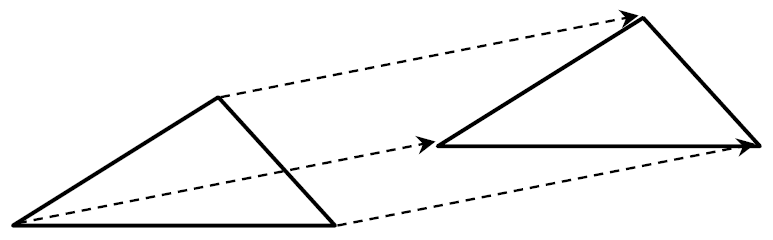
平行移動とは、「ある点を一定の方向に一定の距離だけ動かすこと」です。 高校数学では関数の平行移動というものを考えます。 関数は無数の点の集まりですから、この無数の点を一律に平行移動させると関数自体も平行移動することになります。 今回は、ある関数を平行移動させた結果、どのような関数になるかを求める方法の説明を行っていきます。※ 数学で「~だけ」というときは,「たったそれだけ」「それっぽっち」という意味でなく,「ちょうどそれだけ」という意味に使う. 「 4 だけ平行移動する」などという.




