このとき曲線 r=a(1cosθ) a>0 によって囲まれる領域の重心のx座標を求めよ という問題なんですが まずr=a(1cosθ)によって囲まれる面積を求めてそのあと二重積分を使って求めるということはわかるのですがr=a(1cosθ)によって囲まれる面積の出し方がわかりませ 問題 下図に示す図形の図心を求めよ。 解説 構造力学の基礎的な問題の1つ。図心を求める方法はいくつもありますが、今回は 断面1次モーメントを用いた方法 で解きましょう。 断面1次モーメントは、平面図形内の1点(y,z)を囲む面積要素をdAとして、以下の式で定義される物理量です。 閉じた多角形の重心(図心)位置を求める方法です。 オブジェクトスナップを使用する 線分(line)コマンドを使用して、始点をオブジェクトスナップのを指定して作図します。座標点を確認する場合は、で線分の始点座標を確認します。 リージョンのマスプロパティを確認する

円の切り抜き図形の重心の求め方 公式 そんなの使わんよ 受験物理 Set Up
図形 の 重心 の 求め 方
図形 の 重心 の 求め 方- こんにちは、ウチダです。 今日は数学a「図形の性質」で習う 「三角形の内心」 について、性質の証明や基本的な使い方(角の二等分線と比)、座標の求め方や位置ベクトル表示などをわかりやすく解説していきたいと思います。 外心に関する記事と内容がか 中点の座標の求め方 前記事 →内分点と外分点の求め方 で,線分を内分する点の座標の求め方を解説しました. 線分を 1 1 1 1 に内分する点をその線分の 中点 といいます.中点の座標は次の公式を用いて計算することができます. 中点の座標: 2 2 点 A(x1




高校数学a 三角形の重心1 基本 映像授業のtry It トライイット
図形の性質 三角形の面積公式まとめ! 正三角形の定義は?面積公式、高さや重心についても解説! 三角形の面積の求め方 三角形の面積の求め方について、公式の使い分け早見表や例題を通して説明します。なぜ重心が定まるのか考えよう。 3つの左右が釣り合う直線を描くとき、それらが一点で交わるのはなぜだろうか。 2 天秤、シーソーの釣り合い 「右は釣り合っていますか?」 「板を載せたときの釣り合いと重心の求め方」問題の解答:くり抜いた円盤の重心を求める 例題 半径2Rの円盤から、図のように半径 R 2 の円盤をくりぬいた。 この時、 残った円盤の重心の位置を答えよ。 ※いつも通り、まずは自分で考えてみましょう! 自分で解くことで、『解くうえで何が足り
重心の求め方から応用問題まで徹底解説! │ 受験スタイル 例題付き重心って何? 重心の求め方から応用問題まで徹底解説! なんとなく物体の中心というイメージをもっているのではないでしょうか? 物理基礎でもあまり説明なく、そのように それでは、五心それぞれの定義や性質、求め方をまとめていきます! 重心とは? 重心とは、物質や図形における 重さの中心 のことで、その \(1\) 点で全体をバランスよく支えられる点です。 ここでは、三角形における重心の定義・性質・求め方を説明し平面図形の面積(A) 周長(L) 重心位置(G) 型名 図形 公式 円 扇 形 弓 形 楕 円 方 物 形 三 角 形 平 行 四 辺 形 台 形 四 辺 形 正 n 角 形
図形の重心に対する感覚を豊かにする教材の提案 165 4.指導の展開 (ねらい)長方形の重心を見つける活動を通して,重心の求め方を理解し,それを応用してL字型図形の 重心を求めることができる。※授業内では「重心」を「つり下げられる点」と表現する。 Yの方も同じ手順で求められるので、OpenCVPython Tutorialsで説明されていた 重心は と の関係から求められます。 が成り立つことがわかりました。 理解してみると意外と難しくなかった。。。 6 numpyとscikitimageで試す ・numpyで計算してみる重心の特徴、問題の解き方 重心 とは、 3つの中線が交わる点 のことをいいます。 ※中線とは各頂点から向かい合う辺の中点に向かって引いた線のこと では、重心の特徴についてまとめておきましょう。




パップスギュルダンの定理 数学に物理を添えて 灘校の教室 家庭教師 C O D Club
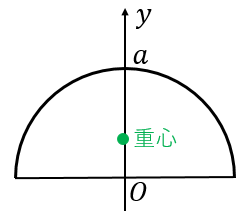



半円の重心の位置を求める公式 具体例で学ぶ数学
これと考え方は同じで面積を考慮した物が下記になります。 X, Y方向をそれぞれ 求めて 図心を出します。 面積 A の図形を考え図心 C を通る直行軸を y, z これに平行な任意の直行軸を y1, z1 とし図形内の微小面積を dA とすれば重心の定義によって図心の求め方 さて、図心の求め方は断面一次モーメントを使うことで簡単に求めることができました。 会の通りです。 Σ(A×y)/ΣA Aは、ある図形の断面積、yは、ある図形の図心位置です。 つまり、断面積と図心位置までの距離を合計した値を、全断で与えられる点である 。 この点は、集合の各点からの平方ユークリッド距離の和を最小化する。 平面図形 X の重心を、図形を有限個のより単純な図形 X 1, X 2, , X n に分割することで計算することができる。 各小図形片 X i の重心を C i, 面積を A i として、 X の重心の各座標は




切り抜かれた円盤の重心 高校物理の備忘録



やさしい実践 機械設計講座
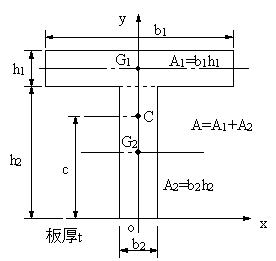
小さく分割し、分割したそれぞれの重心の合力により 重心位置を求めると、右の図のような位置になる。 2つの面の重心位置を結ぶ直線の1/2の距離 底面の重心軸から1/4の高さ 立体形 重心の求め方 重心位置 お役立ち資料集 お役立ち資料集 18 お役立ち資料集となる。作用点l 0 が重心の位置で、断面が一様な棒の場合は中点である。 T型の場合 図形の形状が、重心の位置が既知の図形に分解できるときにはそれぞれの面積と位置から合成することにより全体の形状の重心位置が求められます。7角形の重心を計算しよう。 計算上、最後の3角形の面積計算のため、1番目の点座標を8番目にも設定します。 図4 多角形(ポリゴン)の重心計算 簡単ですね。
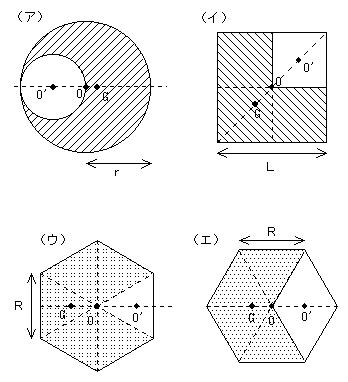



剛体の重心




三角形の重心の座標の求め方とその証明 数学ii By ふぇるまー マナペディア
\ v Z ł Ƃ ̏d S ́A ̏d ʂ v X ܂ B Ⴆ K ̏ \ ʂł A1 K ̉ A K ̂镔 ł Bまた合同条件や、比の計算問題の解き方も詳しく解説していくので、ぜひマスターして この平面図形の重心の求め方が分からないので教えて下さい 図を2分割してそれぞれの重心と面積を求めると図のようになり面積 (重量)比は913S1=1*150=1800S2=100*260=2600S1S2 厳密な重心の求め方 Let's Computer Vision C 便利技 Mochizuki 厳密な重心の求め方 移動体の追跡 や 粒子のカウント のチュートリアル中では輪郭構成点から近似的な中心座標を求める手法を紹介していましたが、今回は厳密な重心を求める手法




扉の質量と重心の求め方




6 柱と梁の断面形と幾何学
平面図形の性質 P12 立体の体積(V),表面積(S)または側面積(F)および重心位置(G) P12 平均自乗誤差 P13 円板の最大応力(σmax)と最大たわみ(ωmax) P96 長柱の座屈 P97 各種断面形の軸のねじり P97 梁の公式 P98 キーの強さ P102公式計算 平面図形の面積(a),周長(l)および重心位置(g) p11 平面図形の性質 p12 立体の体積(v),表面積(s)または側面積(f)および重心位置(g) p12
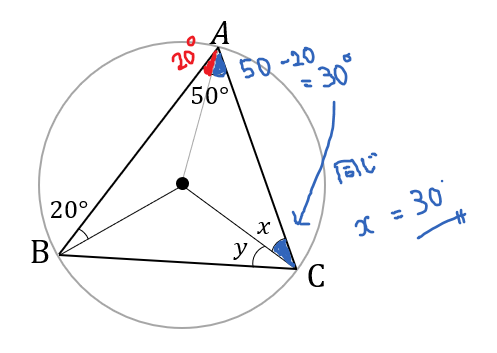



外心 内心 重心の特徴と問題の解き方をサクッとまとめ 数スタ
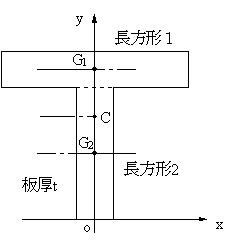



重心の求め方について 重心の求め方について 物体を構成する微小部分には その質量に比例した重力が鉛直下向きに作用します 各々の微小部分に作用する重力は平行な力であり 各々の微小部分に作用する力を合成した合力が物体の重さであり 合力の



2




力学 積分で三角形の重心を求めてみた 公式の証明もあり 物理 プログラミング日記



正五角形の重心はどのようにして見つけますか Quora
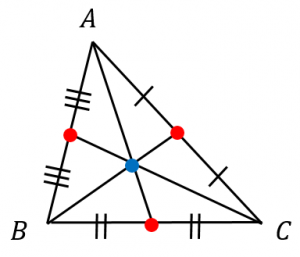



三角形の重心の定義といろいろな求め方 具体例で学ぶ数学
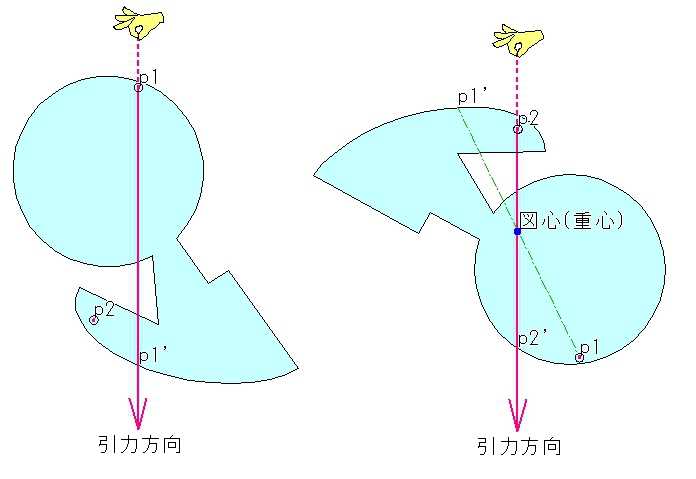



任意の形状の図心の求め方 Hayabusa339のブログ 楽天ブログ




平面図形の面積 A 周長 L および重心位置 G 弓形 P11



2




転倒モーメントがわかる 重心位置との関係と計算方法について バッコ博士の構造塾



1




三角形の重心の性質とその証明 求め方 数学a By となりがトトロ マナペディア



工業高校に通っている高校生です 明後日テストがあるのですが 平面図 Yahoo 知恵袋



平面図形の面積 周長 重心位置の求め方



身体重心の求め方について 義肢装具士の基礎力学




単純閉曲線で囲まれた図形の重心3 二重積分の応用 身勝手な主張




図形の重心を解析的に求める方法 理系のための備忘録




重心の位置を実験で求める方法 軽い平面形状物体 Youtube



積分による重心位置の求め方 わすれなぐさ



重心の求め方について 重心の求め方について 物体を構成する微小部分には その質量に比例した重力が鉛直下向きに作用します 各々の微小部分に作用する重力は平行な力であり 各々の微小部分に作用する力を合成した合力が物体の重さであり 合力の



やさしい実践 機械設計講座



1




断面二次モーメントの求め方 複雑な図形の断面二次モーメントが解ける おりびのブログ
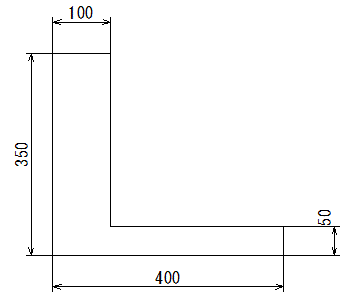



御所実業高校 機械工学科 の日記 第21回 重心 2 問16の解説



1




図形の重心を解析的に求める方法 理系のための備忘録



物体の重心



この平面図形の 重心 を求める方法を 分かりやすく解説して Yahoo 知恵袋




重心を計算して求める 5 Youtube




重心とは何か 座標を使って重心を求める方法 物理 高校生向け受験応援メディア 受験のミカタ
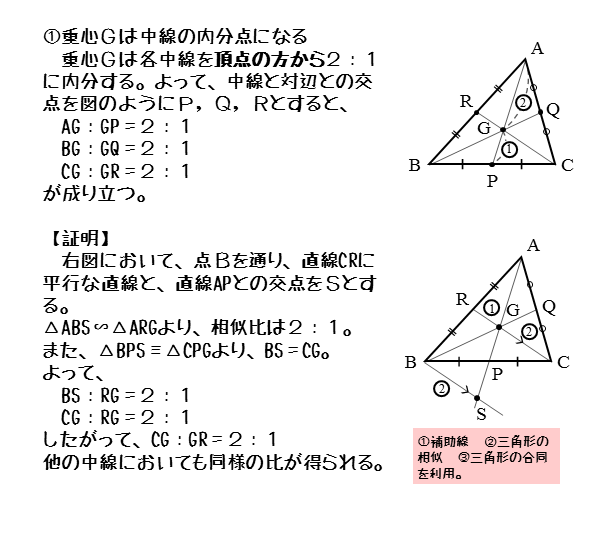



図形の性質 重心について 日々是鍛錬 ひびこれたんれん
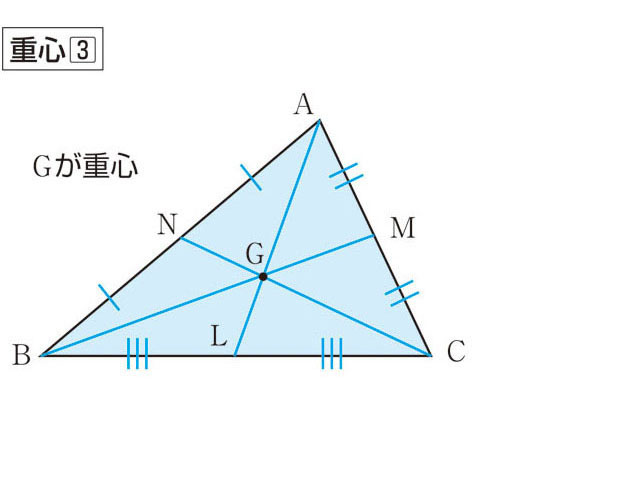



重心とは何 Weblio辞書




高校数学a 三角形の重心1 基本 映像授業のtry It トライイット




円の切り抜き図形の重心の求め方 公式 そんなの使わんよ 受験物理 Set Up
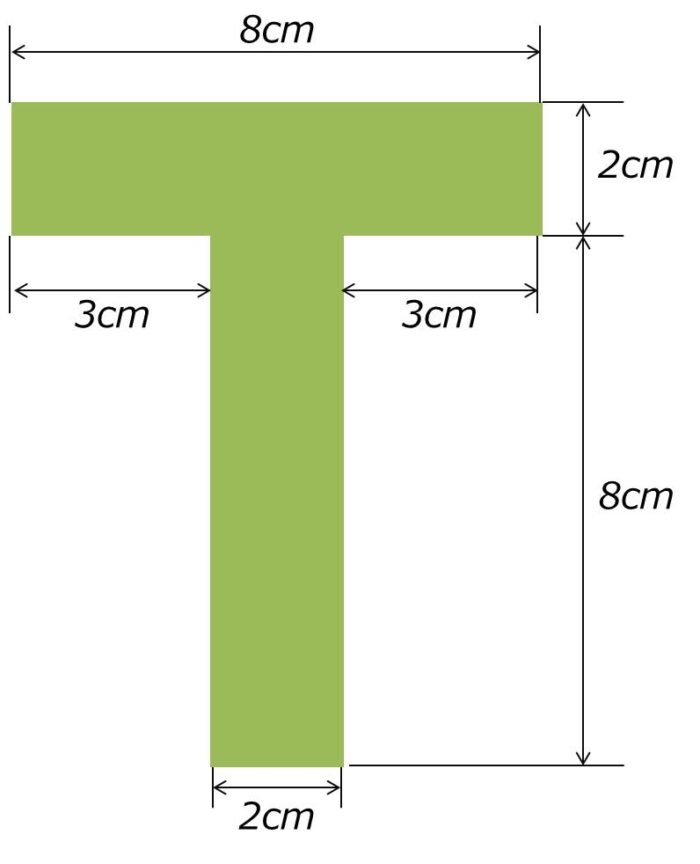



構造力学 断面1次モーメントを用いて図形の図心を求める




重心 高校物理の備忘録




高校物理 難問にこそ現れる 重心 力学 お茶処やまと屋




断面一次モーメントを用いて図心位置を求めてみよう こーりきくん
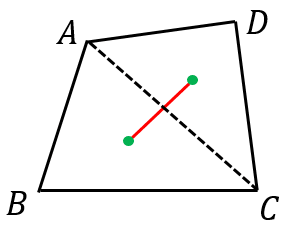



四角形の重心の2通りの求め方と注意点 高校数学の美しい物語



2




家相 風水での建物の中心 図心 重心 の求め方 風水 家相が気になる人の家づくり



Step1 1




2講 三角形の外心 内心 重心 1節 平面図形 問題集 2章 図形の性質
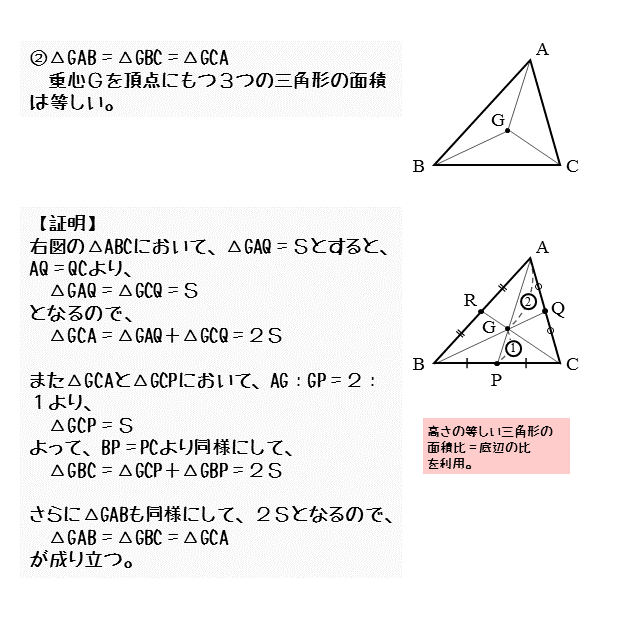



図形の性質 重心について 日々是鍛錬 ひびこれたんれん




四角形の重心の求め方の定義名 図のような四角形の重心の求め方には定 数学 教えて Goo
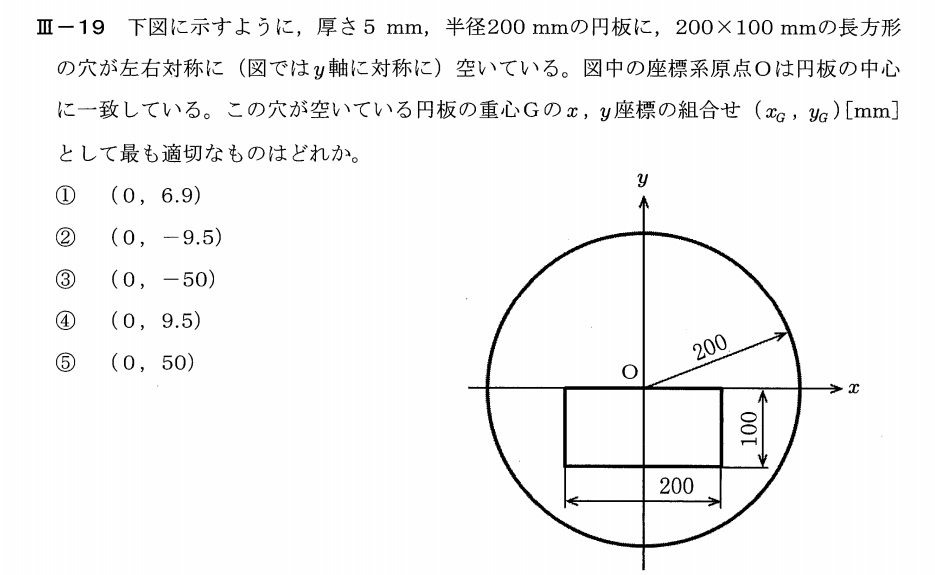



平成25年度技術士第一次試験問題 機械部門 専門科目 19 切り抜かれた円板の重心の求め方 副業の宮殿




図形の重心を解析的に求める方法 理系のための備忘録
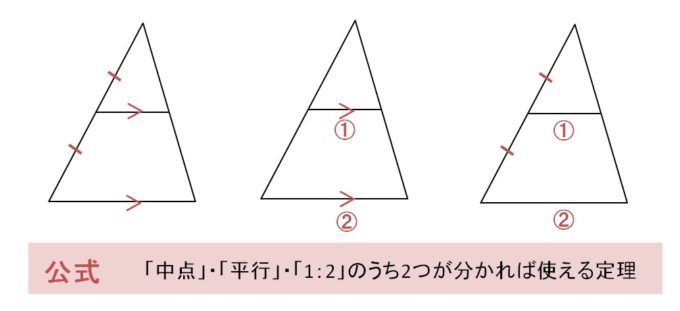



高校入試対策数学 三角形の重心の演習問題 Examee
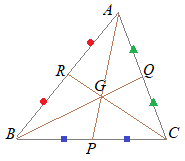



数2 重心
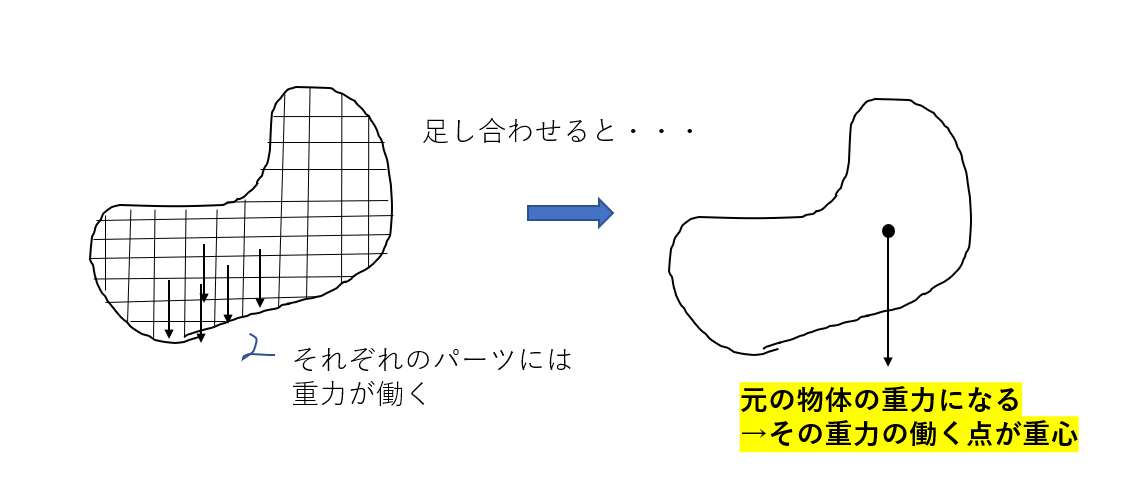



物理の重心とは 重心の求め方に公式はありません 受験物理 Set Up



大至急 コイン100枚 この平面図形の重心の求め方を教 Yahoo 知恵袋
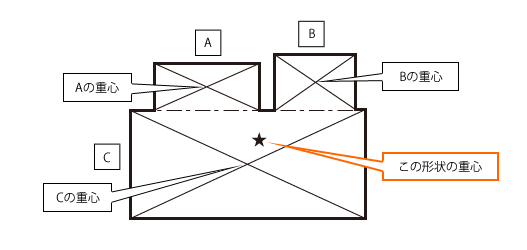



重心について 機械工学と自動機設計 8 技術情報 Misumi Vona ミスミ




学習記録 9 22 重心の求め方を使ってみた 特許翻訳へお引越し



図心ってなに 図心の求め方と断面一次モーメントの関係
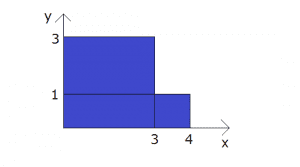



Hiro Academia 偏差値30からの早稲田慶應専門個別指導塾といえば




高校数学 三角形の重心公式 映像授業のtry It トライイット




三角錐の重心 四面体の重心 Schoolmath S Diary
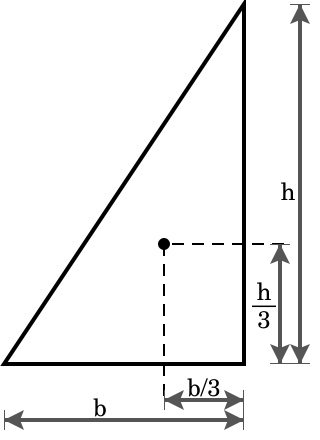



重心の一覧 Wikipedia



図心の求め方



2



3 多角形の重心




土木小ネタ 重心位置 おっさんのblogというブログ



2



重心とは 1分でわかる簡単な意味 定義 求め方 公式



多角形の面積 重心 図心 断面n次モーメントの公式と 向き 頂点列の回転方向 の判別方法
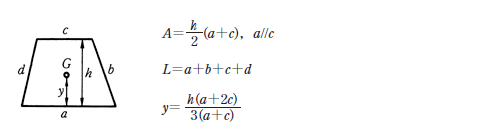



平面図形の面積 A 周長 L および重心位置 G 台形 P11



物体の重心



2



図心の求め方
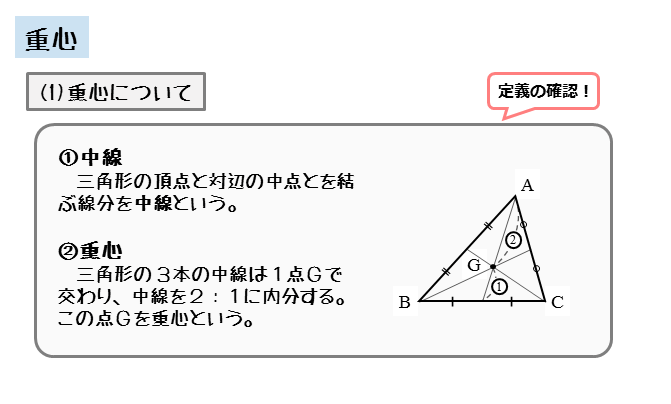



図形の性質 重心について 日々是鍛錬 ひびこれたんれん




三角形の重心 数学ii フリー教材開発コミュニティ Ftext



台形の重心は 1分でわかる意味 重心位置の求め方 面積




5 2 2 中立軸の位置は一次モーメントの計算で求める
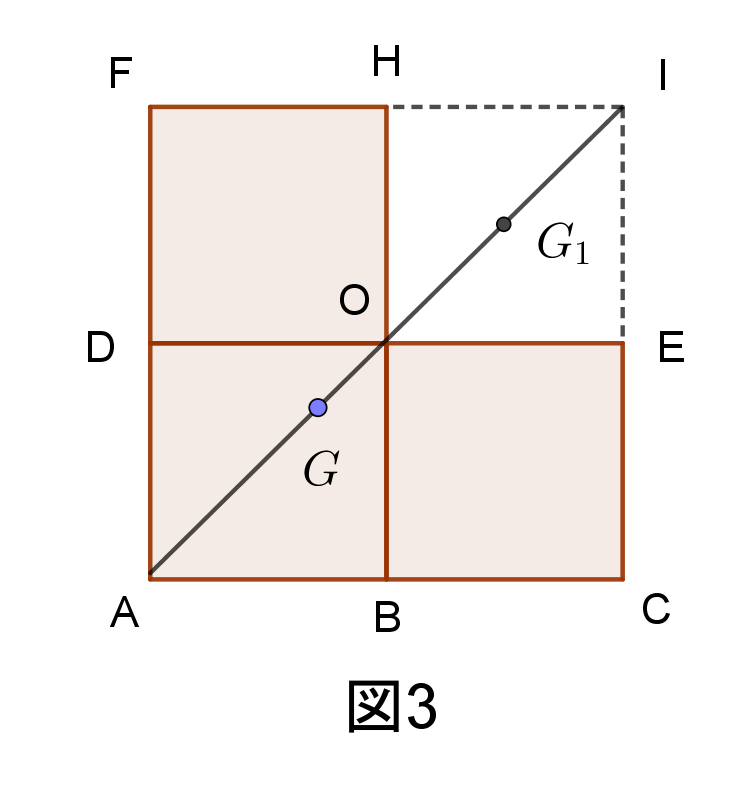



My Math Note



中点と三角形の重心の座標の求め方 思考力を鍛える数学



3 多角形の重心




代表的な図形の重心の公式一覧と導出方法




切り抜かれた円盤の重心 高校物理の備忘録



積分を利用した重心の求め方



図心ってなに 図心の求め方と断面一次モーメントの関係
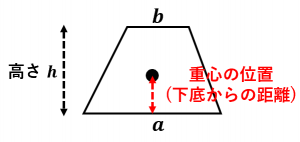



台形の重心を求める公式と導出 具体例で学ぶ数学



1




重心の求め方を教えてください L型の重心を求めたいのですが皆さんの力を貸 Okwave



五心とは 三角形の重心 内心 外心 垂心 傍心の性質と求め方 受験辞典




御所実業高校 機械工学科 の日記 第22回 重心の答え合わせ




図形の重心を解析的に求める方法 理系のための備忘録




例題付き 重心って何 重心の求め方から応用問題まで徹底解説 受験スタイル



重心の軌跡 数学の偏差値を上げて合格を目指す
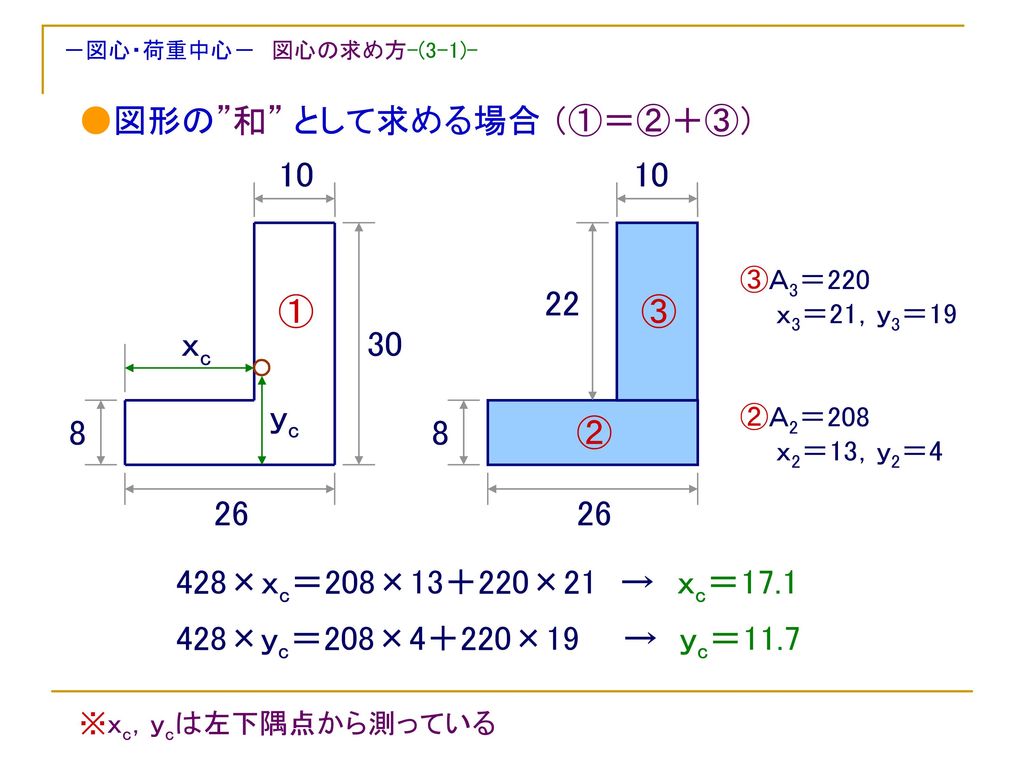



横力f n W 自重 t tf Mn 滑りのメカニズム t 滑動力 すべり面に平行な力 せん断力 Ppt Download



重心を理解する フィジオ八王子
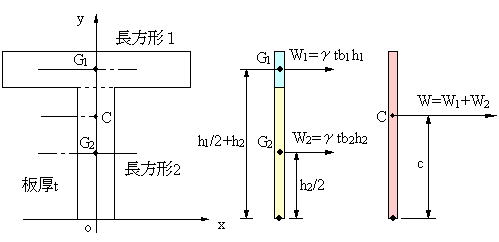



重心の求め方について 重心の求め方について 物体を構成する微小部分には その質量に比例した重力が鉛直下向きに作用します 各々の微小部分に作用する重力は平行な力であり 各々の微小部分に作用する力を合成した合力が物体の重さであり 合力の



物体の重心
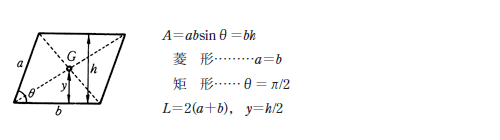



平面図形の面積 A 周長 L および重心位置 G 平行四辺形 P11
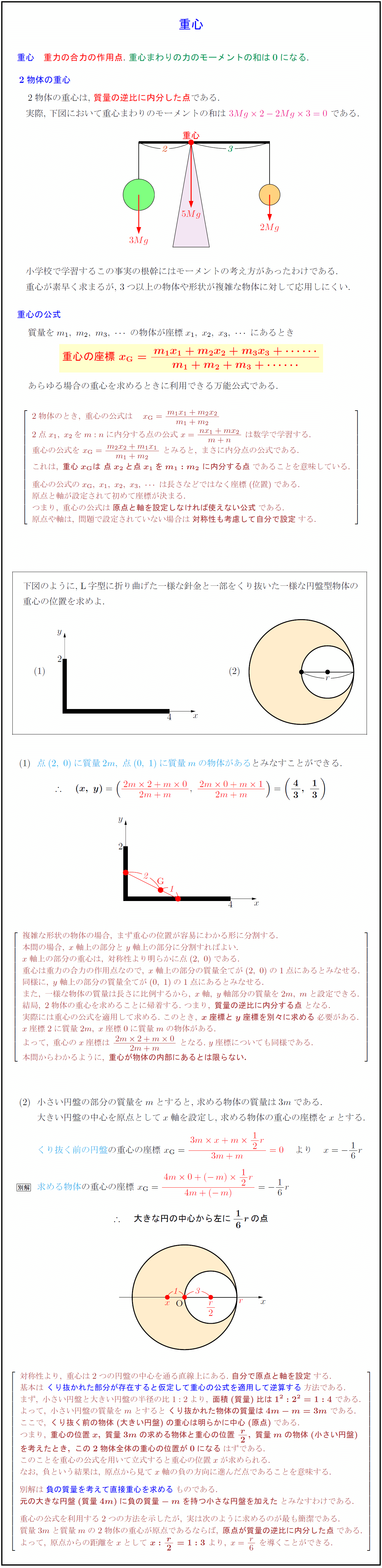



高校物理 剛体の力学 重心 L字型物体 一部がくり抜かれた物体 重心の公式 受験の月



重心 図形 幾何学 数学教育



2


